推荐|【深度学习入门】梯度下降算法

2.2 梯度下降算法改进

学习目标

目标
- 了解深度学习遇到的一些问题
- 知道批梯度下降与MiniBatch梯度下降的区别
- 知道指数加权平均的意义
- 知道动量梯度、RMSProp、Adam算法的公式意义
- 知道学习率衰减方式
- 知道参数初始化策略的意义
应用
- 无

深度学习难以在大数据领域发挥最大效果的一个原因是，在巨大的数据集基础上进行训练速度很慢。而优化算法能够帮助我们快速训练模型，提高计算效率。接下来我么就去看有哪些方法能够解决我们刚才遇到的问题或者类似的问题

2.2.1 优化遇到的问题

梯度消失或者梯度爆炸
局部最优

2.2.1.1 梯度消失

在梯度函数上出现的以指数级递增或者递减的情况分别称为梯度爆炸或者梯度消失。

假设 $g(z) = z, b^{[l]} = 0$ ,对于目标输出有： $\hat{y} = W^{[L]}W^{[L-1]}...W^{[2]}W^{[1]}X$

对于 $W^{[l]}$ 的值大于 1 的情况，激活函数的值将以指数级递增；
对于 $W^{[l]}$ 的值小于 1 的情况，激活函数的值将以指数级递减。

在计算梯度时，根据不同情况梯度函数也会以指数级递增或递减，导致训练导数难度上升，梯度下降算法的步长会变得非常小，需要训练的时间将会非常长。

2.2.1.2 局部最优

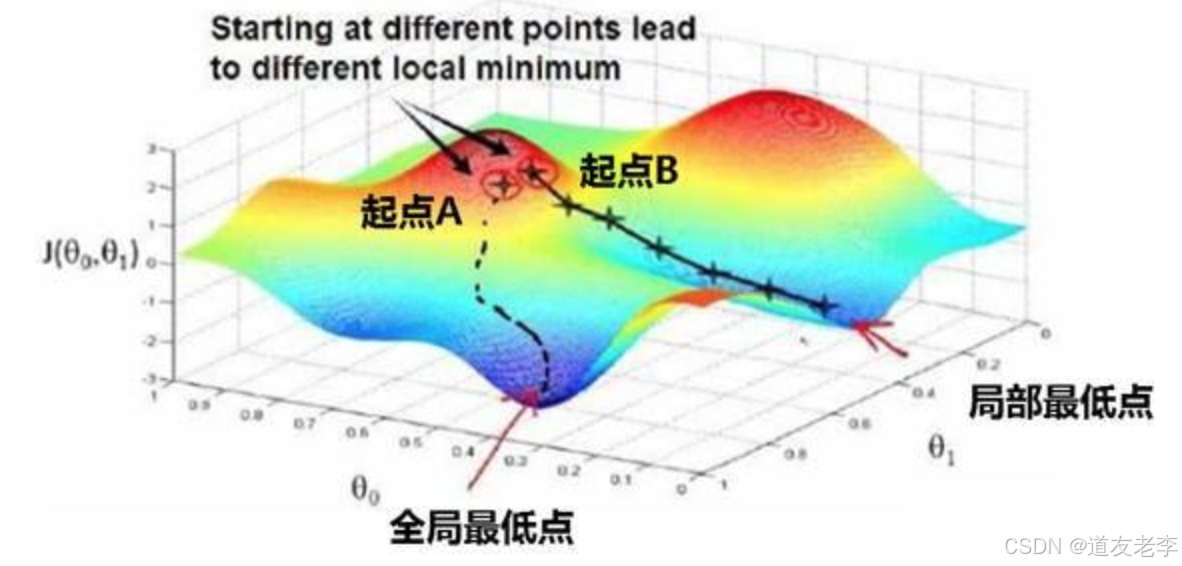
在这里插入图片描述

**鞍点（saddle）**是函数上的导数为零，但是轴上局部极值的点。通常梯度为零的点是上图所示的鞍点，而非局部最小值。减少损失的难度也来自误差曲面中的鞍点，而不是局部最低点。

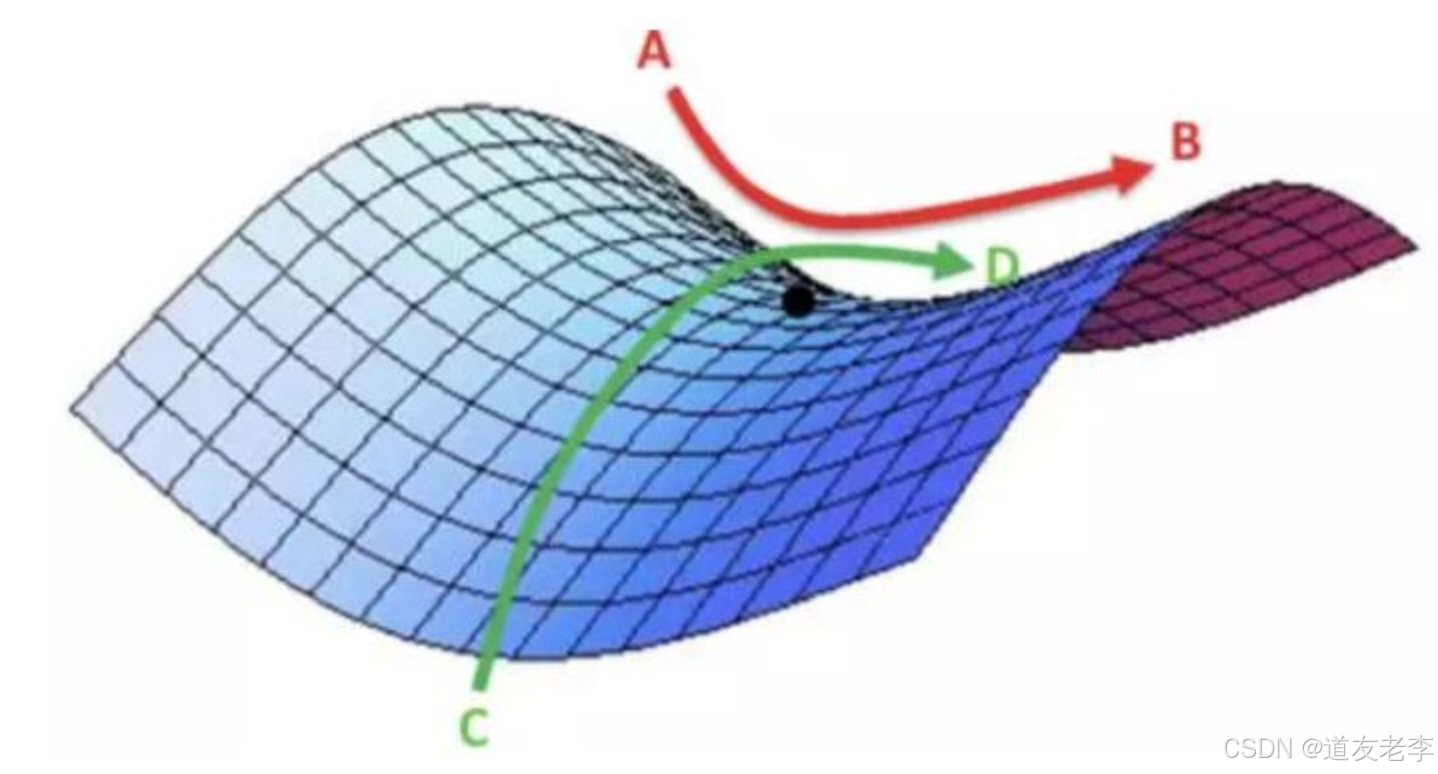
在这里插入图片描述

在训练较大的神经网络、存在大量参数，并且成本函数被定义在较高的维度空间时，困在极差的局部最优基本不会发生
鞍点附近的平稳段会使得学习非常缓慢，而这也是需要后面的动量梯度下降法、RMSProp 以及 Adam 优化算法能够加速学习的原因，它们能帮助尽早走出平稳段。

解决办法有多种形式,通常会结合一些形式一起进行

初始化参数策略（第一部分第四节提到）
Mini梯度下降法
梯度下降算法的优化
学习率衰减

2.2.2 参数初始化策略（复习）

由于在 $z={w}_1{x}_1+{w}_2{x}_2 + ... + {w}_n{x}_n + b$ 公式中，当输入的数量n较大时，如果每个 $w_i$ 的值都大一些，这样它们的和得到的 $z$ 也会非常大，所以会造成我们之前在第一部分最后一节当中介绍的。所以都会初始化比较小的值。

2.2.3 批梯度下降算法（Batch Gradient Descent）

定义：批梯度下降法(batch)，即同时处理整个训练集。

其在更新参数时使用所有的样本来进行更新。对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候，处理速度就会比较慢。

所以换一种方式，每次处理训练数据的一部分进行梯度下降法，则我们的算法速度会执行的更快。

2.2.3.1 Mini-Batch Gradient Descent

定义：Mini-Batch 梯度下降法（小批量梯度下降法）每次同时处理固定大小的数据集。

不同

种类：
- mini-batch 的大小为 1，即是随机梯度下降法（stochastic gradient descent）

使用 Mini-Batch 梯度下降法，对整个训练集的一次遍历(epoch)只做 mini-batch个样本的梯度下降，一直循环整个训练集。

2.2.3.2 批梯度下降与Mini-Batch梯度下降的区别

batch梯度下降法和Mini-batch 梯度下降法代价函数的变化趋势如下：

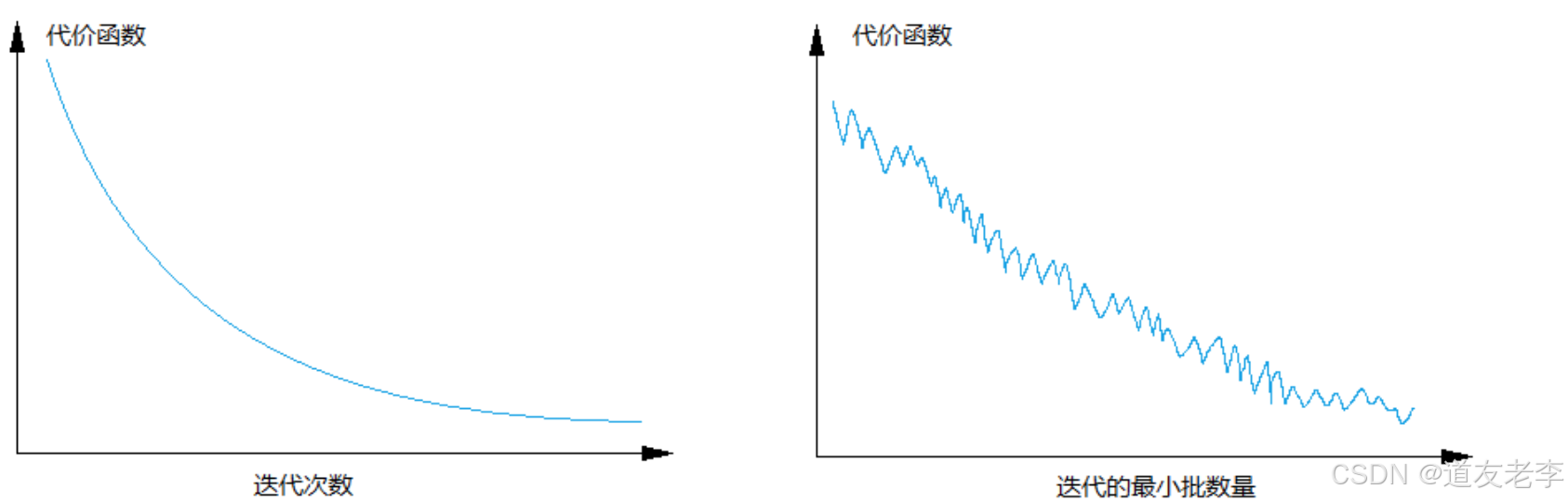
在这里插入图片描述

那么对于梯度下降优化带来的影响

2.2.3.3 梯度下降优化影响

batch 梯度下降法：
- 对所有 m 个训练样本执行一次梯度下降，每一次迭代时间较长，训练过程慢；
- 相对噪声低一些，成本函数总是向减小的方向下降。
随机梯度下降法(Mini-Batch=1)：
- 对每一个训练样本执行一次梯度下降，训练速度快，但丢失了向量化带来的计算加速；
- 有很多噪声，需要适当减小学习率，成本函数总体趋势向全局最小值靠近，但永远不会收敛，而是一直在最小值附近波动。

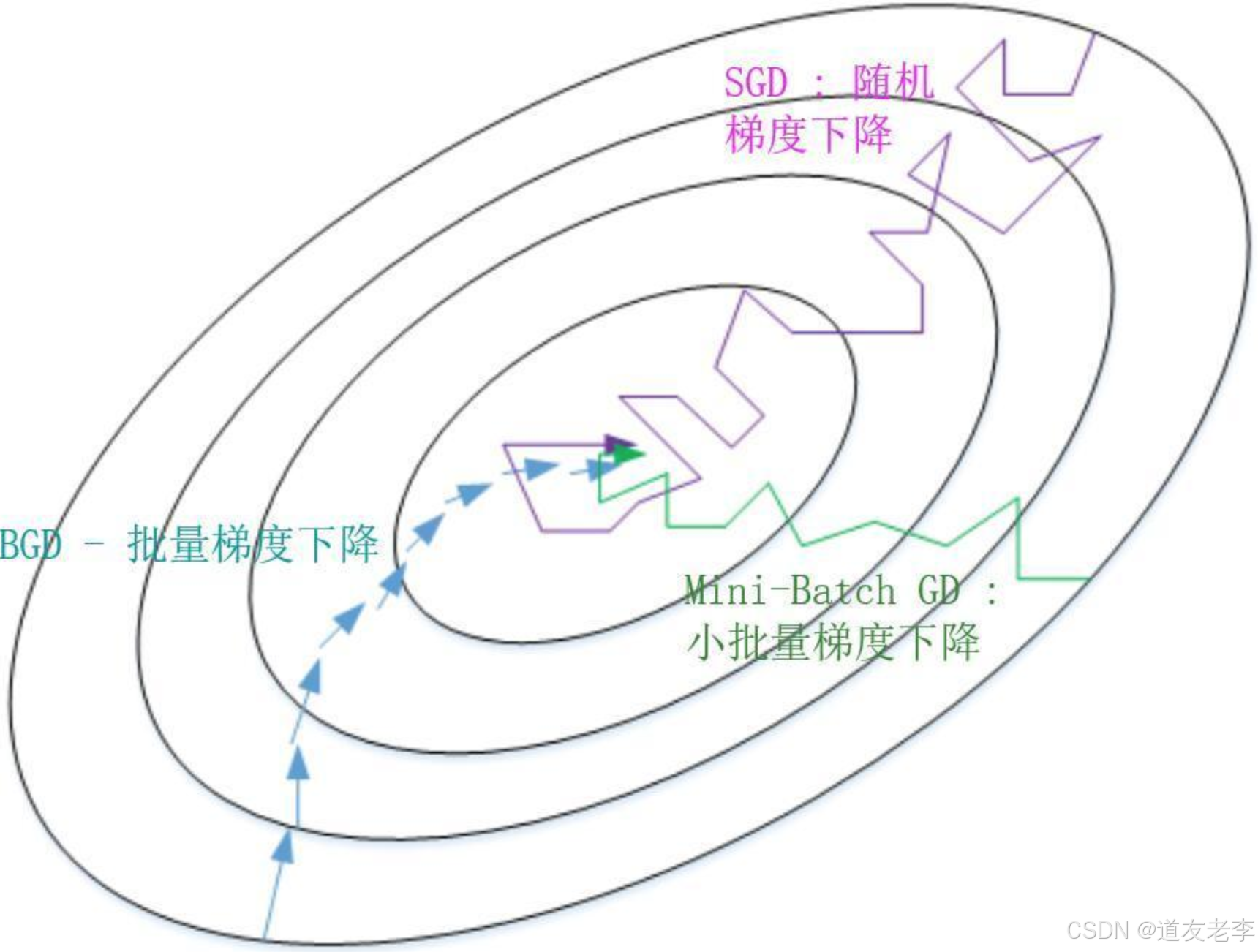
在这里插入图片描述

因此，选择一个合适的大小进行 Mini-batch 梯度下降，可以实现快速学习，也应用了向量化带来的好处，且成本函数的下降处于前两者之间。

2.2.3.4 大小选择

如果训练样本的大小比较小，如 $m\le2000$ 时，选择 batch 梯度下降法；
如果训练样本的大小比较大，选择 Mini-Batch 梯度下降法。为了和计算机的信息存储方式相适应，代码在 mini-batch 大小为 2 的幂次时运行要快一些。典型的大小为 $2^6$ , $2^7,2^8,2^9$ ,mini-batch 的大小要符合 CPU/GPU 内存。

需要根据经验快速尝试，找到能够最有效地减少成本函数的值。

那么第二种方式是通过优化梯度下降过程，会比梯度下降算法的速度更快些

2.2.4 指数加权平均

**指数加权平均（Exponentially Weight Average）**是一种常用的序列数据处理方式，通常用在序列场景如金融序列分析、温度变化序列分析。

假设给定一个序列，例如北京一年每天的气温值，图中蓝色的点代表真实数据。

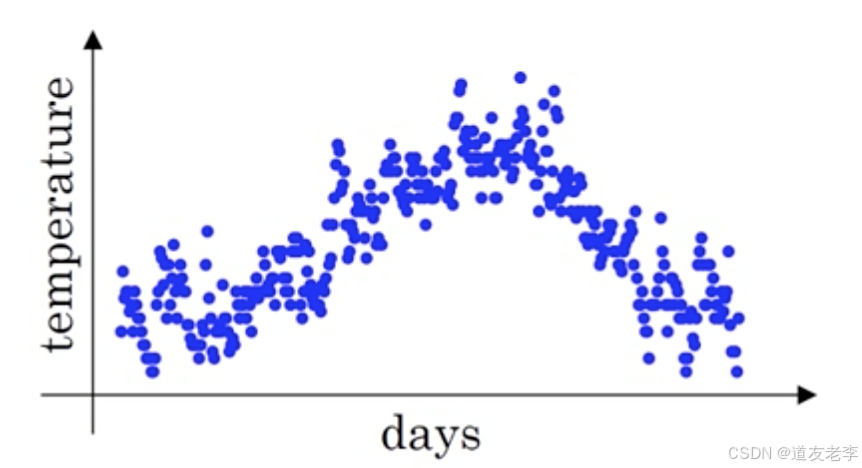
在这里插入图片描述

那么这样的气温值变化可以理解成优化的过程波动较大，异常较多。那么怎么平缓一些呢，这时候就要用到加权平均值了，如指数加权平均值。首先看一些效果。

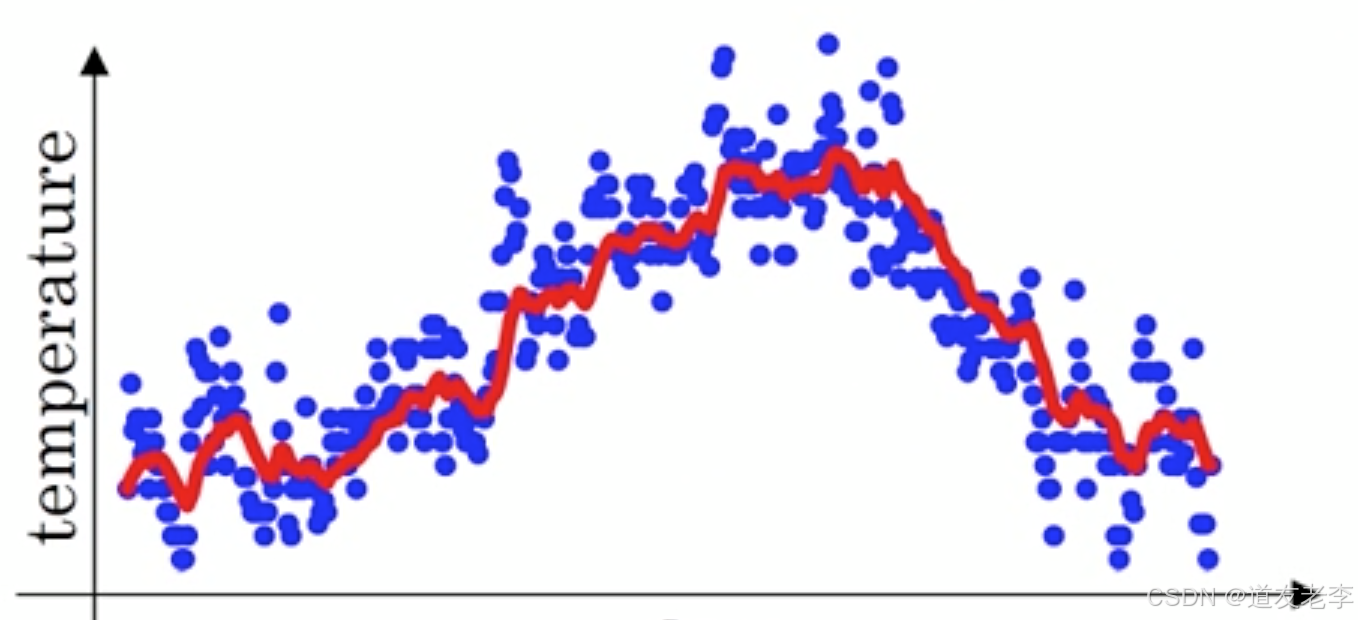
在这里插入图片描述

这条红线怎么计算出来？通过指数加权的公式即：

$S_t =$

{\begin{cases} Y_{1}, & t = 1 \\ β S_{t - 1} + (1 - β) Y_{t}, & t > 1 \end{cases}

$\begin{cases} Y_1, &t = 1 \\ \beta S_{t-1} + (1-\beta)Y_t, &t > 1 \end{cases}$

S_{t} = {Y_{1}, β S_{t - 1} + (1 - β) Y_{t}, t = 1 t > 1

其中 $Y_{t}$ 为 t 下的实际值， $S_{t}$ 为 $t$ 下加权平均后的值， $\beta$ 为权重值。

上图的红线中， $\beta$ 为0.9，那么第一天的温度，第二天的温度，第三天的温度计算为 $S_{1} = Y1$

$S_{2} = 0.9 S_{1} + 0.1 Y_{2}$

…

$S_{99} = 0.9 S_{98} + 0.1 Y_{99}$

$S_{100} = 0.9 S_{99} + 0.1 Y_{100}$

…

假设就100天，那么合并的结果 $S_{100} = 0.1 Y_{100} + 0.1 * 0.9 Y_{99} + 0.1 * {(0.9)}^2 Y_{98} + {...}$

下图中，当取权重值 β=0.98 时，可以得到图中更为平滑的绿色曲线。而当取权重值 $\beta=0.5$ 时，得到图中噪点更多的黄色曲线。 $\beta$ 越大相当于求取平均利用的天数越多**，曲线自然就会越平滑而且越滞后。这些系数被称作**偏差修正（Bias Correction）

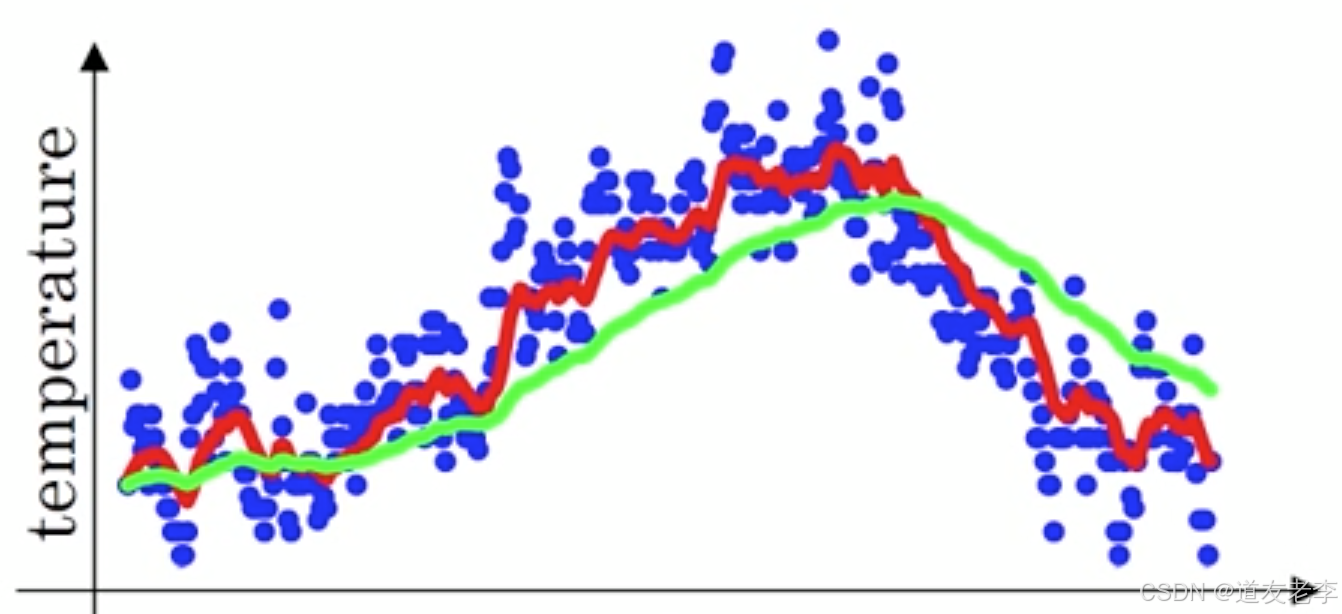
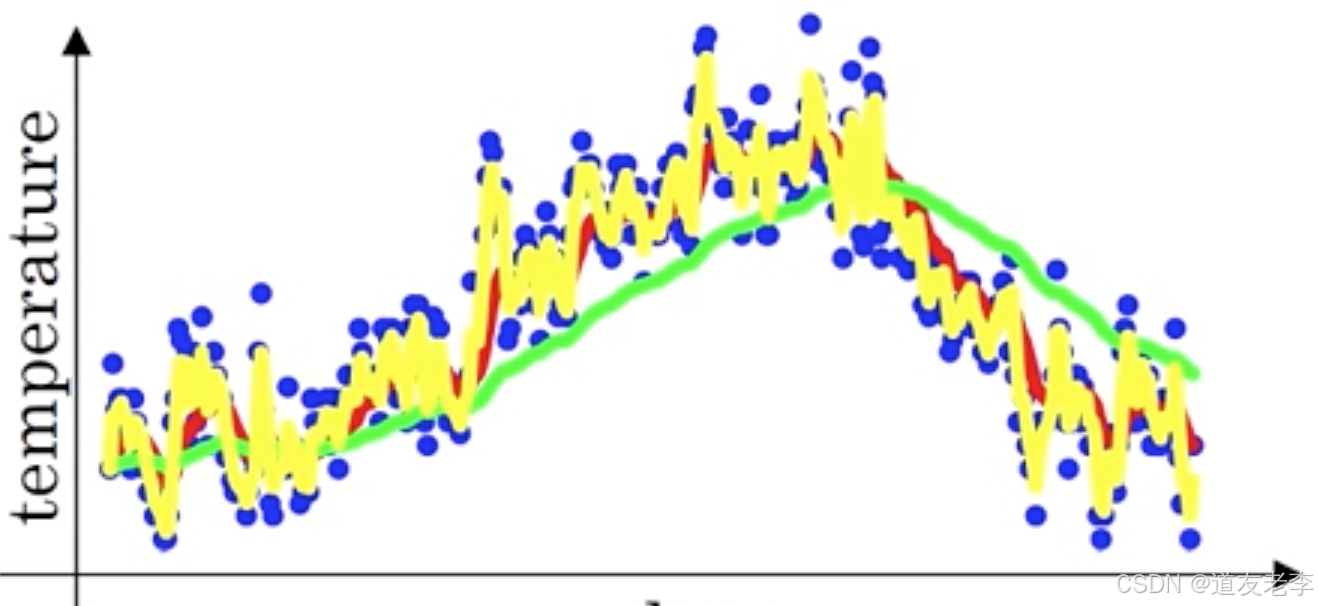
在这里插入图片描述

上述点数据，我们是否可以理解成梯度下降的过程，每一迭代优化计算出来的梯度值，

2.2.5 动量梯度下降法

动量梯度下降（Gradient Descent with Momentum）是计算梯度的指数加权平均数，并利用该值来更新参数值。动量梯度下降法的整个过程为：

$S_{dW^{[l]}} = \beta S_{dW^{[l-1]}} + (1 - \beta) dW^{[l]}$

$S_{db^{[l]}} = \beta S_{db^{[l-1]}} + (1 - \beta) db^{[l]}$

$W^{[l]} := W^{[l]} - \alpha S_{dW^{[l]}}$

$b^{[l]} := b^{[l]} - \alpha S_{db^{[l]}}$

那么这样梯度下降过程会有什么变化，如下图所示：

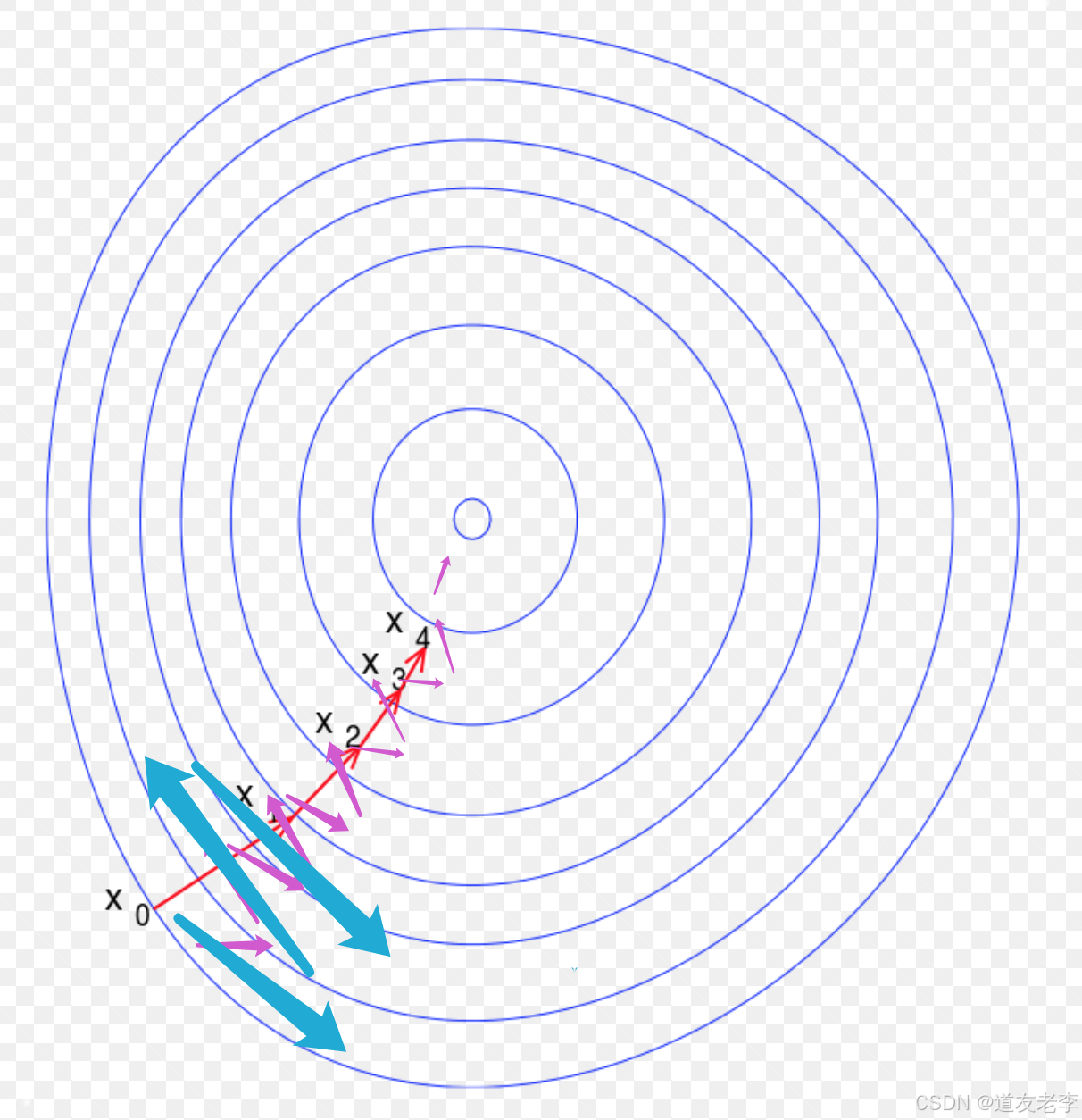
在这里插入图片描述

使用动量梯度下降时，通过累加过去的梯度值来减少抵达最小值路径上的波动，加速了收敛，因此在横轴方向下降得更快，从而得到图中红色或者紫色的曲线。当前后梯度方向一致时，动量梯度下降能够加速学习；而前后梯度方向不一致时，动量梯度下降能够抑制震荡。

我们可以这样形象的理解，小球在向下运动过程中会有加速度，导致越来越快，由于β的存在使得不会一直加速运行。

2.2.6 RMSProp 算法

**RMSProp（Root Mean Square Prop）**算法是在对梯度进行指数加权平均的基础上，引入平方和平方根。

$s_{dw} = \beta s_{dw-1} + (1 - \beta)(dw)^2$

$s_{db} = \beta s_{db-1} + (1 - \beta)(db)^2$

$\alpha \frac{dw}{\sqrt{s_{dw} + \epsilon}}$

$\alpha \frac{db}{\sqrt{s_{db} + \epsilon}}$

其中 $\epsilon$ 是一个非常小的数，防止分母太小导致不稳定,当 $d w$ 或$ db $较大时，$ (dw)^{2}, (db)^{2} $, ($ db $) 2 会较大，进而$ s_dw $* 也会较大，最终使得$ \frac{db}{\sqrt{s_{db} + \epsilon}}$等结果变得非常小。

最终RMSProp 有助于减少抵达最小值路径上的摆动，并允许使用一个更大的学习率 α，从而加快算法学习速度。

2.2.7 Adam算法

**Adam 优化算法（Adaptive Moment Estimation，自适应矩估计）**将 Momentum 和 RMSProp 算法结合在一起。

假设用每一个 mini-batch 计算 dW、db，第t次迭代时：

$v_{dW} = \beta_1 v_{dW-1} + (1 - \beta_1) dW$

$v_{db} = \beta_1 v_{db-1} + (1 - \beta_1) db$

$v^{corrected}_{dW^{[l]}} = \frac{v_{dW^{[l]}}}{1 - (\beta_1)^t}$

$s_{dW} = \beta_2 s_{dW} + (1 - \beta_2) {(dW)}^2$

$s_{db} = \beta_2 s_{db} + (1 - \beta_2) {(db)}^2$

$s^{corrected}_{dW^{[l]}} = \frac{s_{dW^{[l]}}}{1 - (\beta_2)^t}$

其中l为某一层，t为移动平均第次的值

Adam 算法的参数更新：

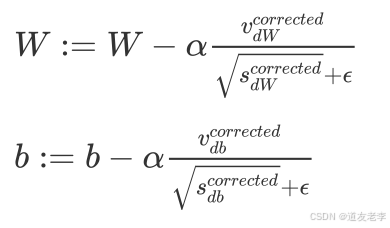
在这里插入图片描述

2.2.8 TensorFlow Adam算法API

tf.train.AdamOptimizer(learning_rate=0.001, beta1=0.9, beta2=0.999,epsilon=1e-08,name=‘Adam’)

Adam 优化算法有很多的超参数:

学习率α：需要尝试一系列的值，来寻找比较合适的
β1：常用的缺省值为 0.9
β2：Adam 算法的作者建议为 0.999
ϵ：Adam 算法的作者建议为epsilon的默认值1e-8

注：β1、β2、ϵ 通常不需要调试

2.2.9 学习率衰减

如果设置一个固定的学习率 α

在最小值点附近，由于不同的 batch 中存在一定的噪声，因此不会精确收敛，而是始终在最小值周围一个较大的范围内波动。
如果随着时间慢慢减少学习率 α 的大小，在初期 α 较大时，下降的步长较大，能以较快的速度进行梯度下降；而后期逐步减小 α 的值，即减小步长，有助于算法的收敛，更容易接近最优解。

最常用的学习率衰减方法： $\alpha = \frac{1}{1 + decay\_rate * epoch\_num} * \alpha_0$

其中，decay_rate为衰减率（超参数），epoch_num为将所有的训练样本完整过一遍的次数。

还有一种指数衰减

$\alpha = 0.95^{epoch\_num} * \alpha_0$

对于大型的数据模型，需要使用这些方式去自动进行学习率衰减。而一些小型网络可以直接手动进行调整

那么最后我们来看一张动态度，表示不同优化的算法的效果图

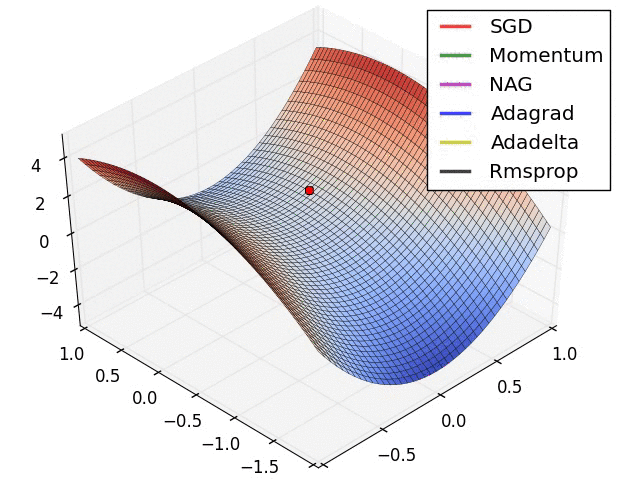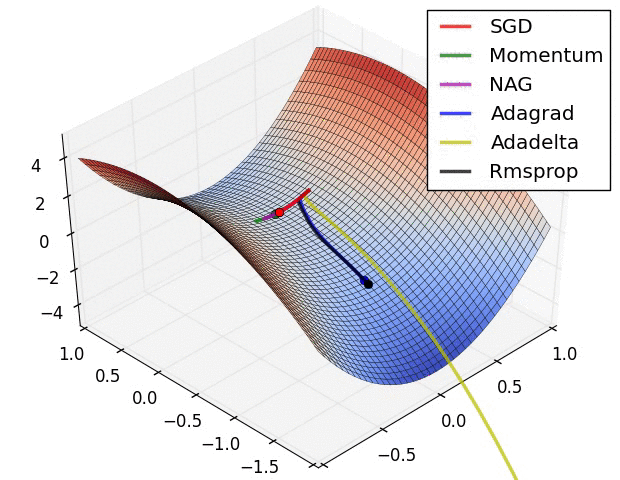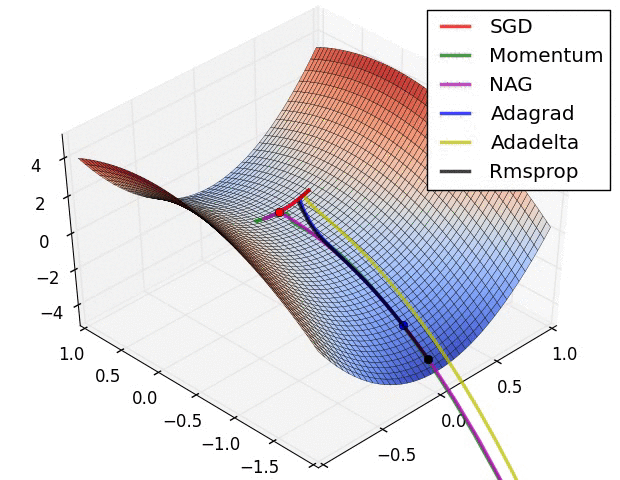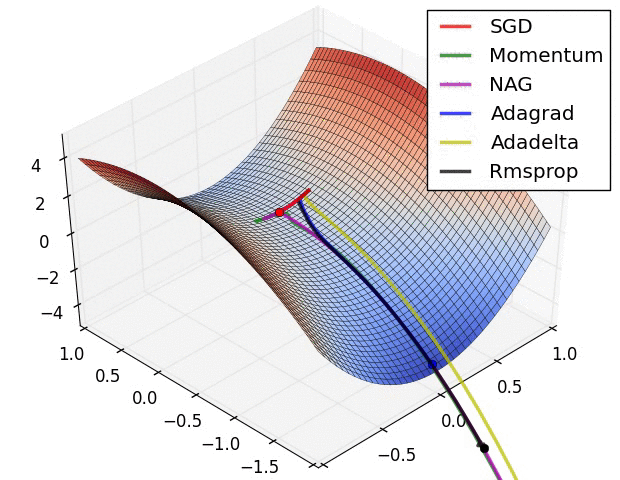
在这里插入图片描述

2.2.10 其它非算法优化的方式-标准化输入

对网络输入的特征进行标准化，能够缓解梯度消失或者梯度爆炸

标准化公式：
- $\frac{x - \mu}{\sigma}$

这个公式其实与特征工程中的处理是一样的，μ为平均值，σ为标准差。标准化的目的是所有特征的平均值为0,标准差为1。这属于机器学习基本的内容不过多进行叙述。

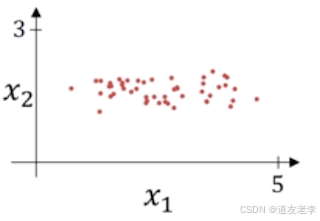
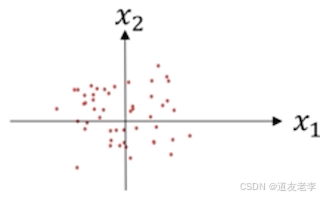
在这里插入图片描述

那么这种有什么好处？主要是对于损失函数带来的好处.

标准化前的损失函数

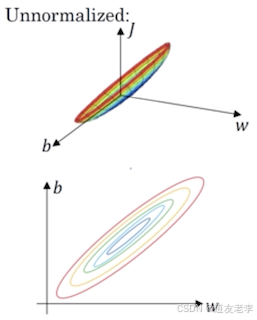
在这里插入图片描述

标准化后的损失函数

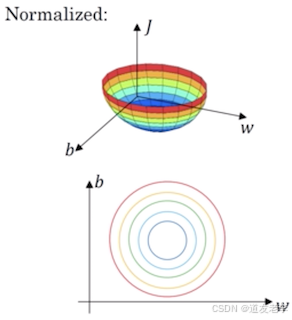
在这里插入图片描述

这样的话，对于梯度下降无论从哪个位置开始迭代，都能以相对较少的迭代次数找到全局最优解。可以加速网络的学习。

理解这个原理，其实还是最初的这样的公式： $z={w}_1{x}_1+{w}_2{x}_2 + ... + {w}_n{x}_n + b$

如果激活函数的输入X近似设置成均值为 0，标准方差为 1，神经元输出 z 的方差就正则化到1了。虽然没有解决梯度消失和爆炸的问题，但其在一定程度上确实减缓了梯度消失和爆炸的速度。

2.2.11 总结

掌握参数初始化策略的优点
掌握Mini-batch的特点以及优势
掌握梯度下降算法优化的目的以及效果
- 掌握指数移动平均值的好处
- 掌握动量梯度下降法的优点以及RMSProp、Adam的特点
- 掌握学习率衰减方式
掌握标准化输入带来的网络学习速度的提升

完整代码

主函数

import numpy as np
import matplotlib.pyplot as plt
import math
import sklearn
import sklearn.datasets

from utils import initialize_parameters, forward_propagation, compute_cost, backward_propagation
from utils import load_dataset, predict


def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
    """
    创建每批次固定数量特征值和目标值
    """

    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []

    # 对所有数据进行打乱
    permutation = list(np.random.permutation(m))

    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1, m))

    # 循环将每批次数据按照固定格式装进列表当中
    num_complete_minibatches = math.floor(
        m / mini_batch_size)

    # 所有训练数据分成多少组
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    # 最后剩下的样本数量mini-batch < mini_batch_size
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size:]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches


def initialize_momentum(parameters):
    """
    初始化网络中每一层的动量梯度下降的指数加权平均结果参数
    parameters['W' + str(l)] = Wl
    parameters['b' + str(l)] = bl
    return:
    v['dW' + str(l)] = velocity of dWl
    v['db' + str(l)] = velocity of dbl
    """
    # 得到网络的层数
    L = len(parameters) // 2
    v = {}

    # 初始化动量参数
    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
        v["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)

    return v


def update_parameters_with_momentum(parameters, gradients, v, beta, learning_rate):
    """
    动量梯度下降算法实现
    """
    # 得到网络的层数
    L = len(parameters) // 2

    # 动量梯度参数更新
    for l in range(L):

        # 开始
        v["dW" + str(l + 1)] = beta * v['dW' + str(l + 1)] + (1 - beta) * (gradients['dW' + str(l + 1)])
        v["db" + str(l + 1)] = beta * v['db' + str(l + 1)] + (1 - beta) * (gradients['db' + str(l + 1)])
        parameters["W" + str(l + 1)] = parameters['W' + str(l + 1)] - learning_rate * v['dW' + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters['b' + str(l + 1)] - learning_rate * v['db' + str(l + 1)]
        # 结束

    return parameters, v


def initialize_adam(parameters):
    """
    初始化Adam算法中的参数
    """
    # 得到网络的参数
    L = len(parameters) // 2
    v = {}
    s = {}

    # 利用输入，初始化参数v,s
    for l in range(L):

        v["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
        v["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)
        s["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
        s["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)

    return v, s


def update_parameters_with_adam(parameters, gradients, v, s, t, learning_rate=0.01,
                                beta1=0.9, beta2=0.999, epsilon=1e-8):
    """
    更新Adam算法网络的参数
    """
    # 网络大小
    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}

    # 更新所有参数
    for l in range(L):
        # 对梯度进行移动平均计算. 输入: "v, gradients, beta1". 输出: "v".
        # 开始
        v["dW" + str(l + 1)] = beta1 * v['dW' + str(l + 1)] + (1 - beta1) * gradients['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v['db' + str(l + 1)] + (1 - beta1) * gradients['db' + str(l + 1)]
        # 结束

        # 计算修正结果. 输入: "v, beta1, t". 输出: "v_corrected".
        # 开始
        v_corrected["dW" + str(l + 1)] = v['dW' + str(l + 1)] / (1 - np.power(beta1, t))
        v_corrected["db" + str(l + 1)] = v['db' + str(l + 1)] / (1 - np.power(beta1, t))
        # 结束

        # 平方梯度的移动平均值. 输入: "s, gradients, beta2". 输出: "s".
        # 开始
        s["dW" + str(l + 1)] = beta2 * s['dW' + str(l + 1)] + (1 - beta2) * np.power(gradients['dW' + str(l + 1)], 2)
        s["db" + str(l + 1)] = beta2 * s['db' + str(l + 1)] + (1 - beta2) * np.power(gradients['db' + str(l + 1)], 2)
        # 结束

        # 计算修正的结果. 输入: "s, beta2, t". 输出: "s_corrected".
        # 开始
        s_corrected["dW" + str(l + 1)] = s['dW' + str(l + 1)] / (1 - np.power(beta2, t))
        s_corrected["db" + str(l + 1)] = s['db' + str(l + 1)] / (1 - np.power(beta2, t))
        # 结束

        # 更新参数. 输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
        # 开始
        parameters["W" + str(l + 1)] = parameters['W' + str(l + 1)] - learning_rate * v_corrected[
            'dW' + str(l + 1)] / np.sqrt(s_corrected['dW' + str(l + 1)] + epsilon)
        parameters["b" + str(l + 1)] = parameters['b' + str(l + 1)] - learning_rate * v_corrected[
            'db' + str(l + 1)] / np.sqrt(s_corrected['db' + str(l + 1)] + epsilon)
        # 结束

    return parameters, v, s


def model(X, Y, optimizer, learning_rate=0.0007, mini_batch_size=64, beta=0.9,
          beta1=0.9, beta2=0.999, epsilon=1e-8, num_epochs=10000, print_cost=True):
    """
    模型逻辑
    定义一个三层网络（不包括输入层）
    第一个隐层：5个神经元
    第二个隐层：2个神经元
    输出层：1个神经元
    """
    # 计算网络的层数
    layers_dims = [train_X.shape[0], 5, 2, 1]

    L = len(layers_dims)
    costs = []
    t = 0
    seed = 10

    # 初始化网络结构
    parameters = initialize_parameters(layers_dims)

    # 初始化优化器参数
    if optimizer == "momentum":
        v = initialize_momentum(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)

    # 优化逻辑
    for i in range(num_epochs):

        # 每次迭代所有样本顺序打乱不一样
        seed = seed + 1
        # 获取每批次数据
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)

        # 开始

        for minibatch in minibatches:

            # Mini-batch每批次的数据
            (minibatch_X, minibatch_Y) = minibatch

            # 前向传播minibatch_X, parameters，返回a3, caches
            a3, caches = forward_propagation(minibatch_X, parameters)

            # 计算损失，a3, minibatch_Y，返回cost
            cost = compute_cost(a3, minibatch_Y)

            # 反向传播，返回梯度
            gradients = backward_propagation(minibatch_X, minibatch_Y, caches)

            # 更新参数
            if optimizer == "momentum":

                parameters, v = update_parameters_with_momentum(parameters, gradients, v, beta, learning_rate)

            elif optimizer == "adam":
                t = t + 1
                parameters, v, s = update_parameters_with_adam(parameters, gradients, v, s,
                                                               t, learning_rate, beta1, beta2, epsilon)

        # 结束

        # 每个1000批次打印损失
        if print_cost and i % 1000 == 0:
            print("第 %i 次迭代的损失值: %f" % (i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)

    # 画出损失的变化
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("损失图")
    plt.show()

    return parameters


if __name__ == '__main__':

    train_X, train_Y = load_dataset()

    parameters = model(train_X, train_Y, optimizer="momentum")

    predictions = predict(train_X, train_Y, parameters)

工具类代码

import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy.io
import sklearn
import sklearn.datasets


def sigmoid(x):
    """
    Compute the sigmoid of x

    Arguments:
    x -- A scalar or numpy array of any size.

    Return:
    s -- sigmoid(x)
    """
    s = 1/(1+np.exp(-x))
    return s


def relu(x):
    """
    Compute the relu of x

    Arguments:
    x -- A scalar or numpy array of any size.

    Return:
    s -- relu(x)
    """
    s = np.maximum(0,x)
    
    return s


def initialize_parameters(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    b1 -- bias vector of shape (layer_dims[l], 1)
                    Wl -- weight matrix of shape (layer_dims[l-1], layer_dims[l])
                    bl -- bias vector of shape (1, layer_dims[l])
                    
    Tips:
    - For example: the layer_dims for the "Planar Data classification model" would have been [2,2,1]. 
    This means W1's shape was (2,2), b1 was (1,2), W2 was (2,1) and b2 was (1,1). Now you have to generalize it!
    - In the for loop, use parameters['W' + str(l)] to access Wl, where l is the iterative integer.
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims) # number of layers in the network

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*  np.sqrt(2 / layer_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
        
        assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])
        assert(parameters['W' + str(l)].shape == layer_dims[l], 1)
        
    return parameters


def compute_cost(a3, Y):
    
    """
    Implement the cost function
    
    Arguments:
    a3 -- post-activation, output of forward propagation
    Y -- "true" labels vector, same shape as a3
    
    Returns:
    cost - value of the cost function
    """
    m = Y.shape[1]
    
    logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
    cost = 1./m * np.sum(logprobs)
    
    return cost


def forward_propagation(X, parameters):
    """
    Implements the forward propagation (and computes the loss) presented in Figure 2.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape ()
                    b1 -- bias vector of shape ()
                    W2 -- weight matrix of shape ()
                    b2 -- bias vector of shape ()
                    W3 -- weight matrix of shape ()
                    b3 -- bias vector of shape ()
    
    Returns:
    loss -- the loss function (vanilla logistic loss)
    """
    
    # retrieve parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    z1 = np.dot(W1, X) + b1
    a1 = relu(z1)
    z2 = np.dot(W2, a1) + b2
    a2 = relu(z2)
    z3 = np.dot(W3, a2) + b3
    a3 = sigmoid(z3)
    
    cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)
    
    return a3, cache


def backward_propagation(X, Y, cache):
    """
    Implement the backward propagation presented in figure 2.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
    cache -- cache output from forward_propagation()
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    m = X.shape[1]
    (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cache
    
    dz3 = 1./m * (a3 - Y)
    dW3 = np.dot(dz3, a2.T)
    db3 = np.sum(dz3, axis=1, keepdims = True)
    
    da2 = np.dot(W3.T, dz3)
    dz2 = np.multiply(da2, np.int64(a2 > 0))
    dW2 = np.dot(dz2, a1.T)
    db2 = np.sum(dz2, axis=1, keepdims = True)
    
    da1 = np.dot(W2.T, dz2)
    dz1 = np.multiply(da1, np.int64(a1 > 0))
    dW1 = np.dot(dz1, X.T)
    db1 = np.sum(dz1, axis=1, keepdims = True)
    
    gradients = {"dz3": dz3, "dW3": dW3, "db3": db3,
                 "da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,
                 "da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}
    
    return gradients


def predict(X, y, parameters):
    """
    This function is used to predict the results of a  n-layer neural network.
    
    Arguments:
    X -- data set of examples you would like to label
    parameters -- parameters of the trained model
    
    Returns:
    p -- predictions for the given dataset X
    """
    
    m = X.shape[1]
    p = np.zeros((1,m), dtype = np.int)
    
    # Forward propagation
    a3, caches = forward_propagation(X, parameters)
    
    # convert probas to 0/1 predictions
    for i in range(0, a3.shape[1]):
        if a3[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0

    print("Accuracy: "  + str(np.mean((p[0,:] == y[0,:]))))
    
    return p


def load_dataset():
    np.random.seed(3)
    train_X, train_Y = sklearn.datasets.make_moons(n_samples=300, noise=.2)
    train_X = train_X.T
    train_Y = train_Y.reshape((1, train_Y.shape[0]))
    return train_X, train_Y

【深度学习入门】梯度下降算法

文章目录

2.2 梯度下降算法改进

学习目标

2.2.1 优化遇到的问题

2.2.1.1 梯度消失

2.2.1.2 局部最优

2.2.2 参数初始化策略（复习）

2.2.3 批梯度下降算法（Batch Gradient Descent）

2.2.3.1 Mini-Batch Gradient Descent

2.2.3.2 批梯度下降与Mini-Batch梯度下降的区别

2.2.3.3 梯度下降优化影响

2.2.3.4 大小选择

2.2.4 指数加权平均

2.2.5 动量梯度下降法

2.2.6 RMSProp 算法

2.2.7 Adam算法

2.2.8 TensorFlow Adam算法API

2.2.9 学习率衰减

2.2.10 其它非算法优化的方式-标准化输入

2.2.11 总结

完整代码

主函数

工具类代码

评论记录：