1.4 深层神经网络

学习目标

• 目标
  • 了解深层网络的前向传播与反向传播的过程
• 应用
  • 图片识别等

为什么使用深层网络

对于人脸识别等应用，神经网络的第一层从原始图片中提取人脸的轮廓和边缘，每个神经元学习到不同边缘的信息；网络的第二层将第一层学得的边缘信息组合起来，形成人脸的一些局部的特征，例如眼睛、嘴巴等；后面的几层逐步将上一层的特征组合起来，形成人脸的模样。随着神经网络层数的增加，特征也从原来的边缘逐步扩展为人脸的整体，由整体到局部，由简单到复杂。层数越多，那么模型学习的效果也就越精确。

通过例子可以看到，随着神经网络的深度加深，模型能学习到更加复杂的问题，功能也更加强大。

1.4.1 深层神经网络表示

1.4.1.1 什么是深层网络？

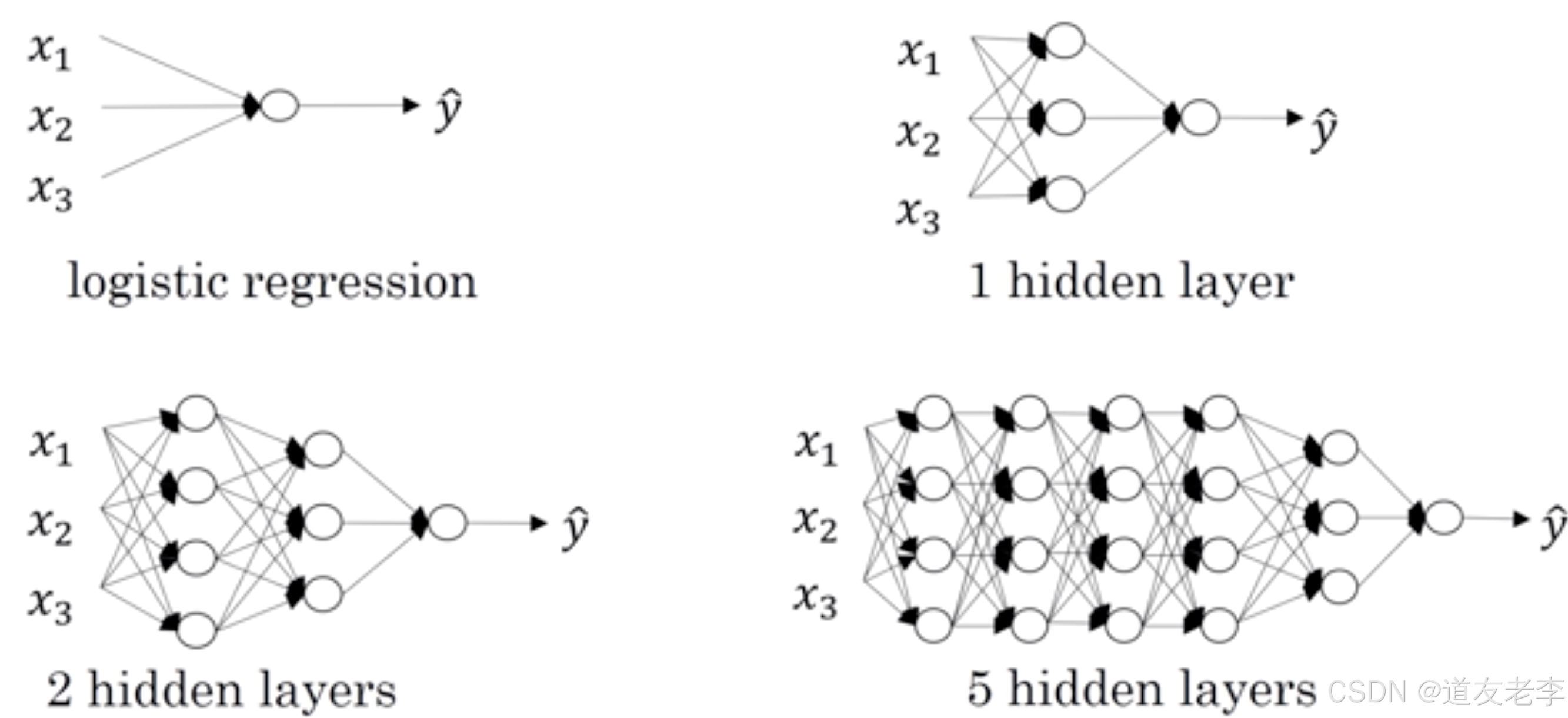
使用浅层网络的时候很多分类等问题得不到很好的解决，所以需要深层的网络。

1.4.2 四层网络的前向传播与反向传播

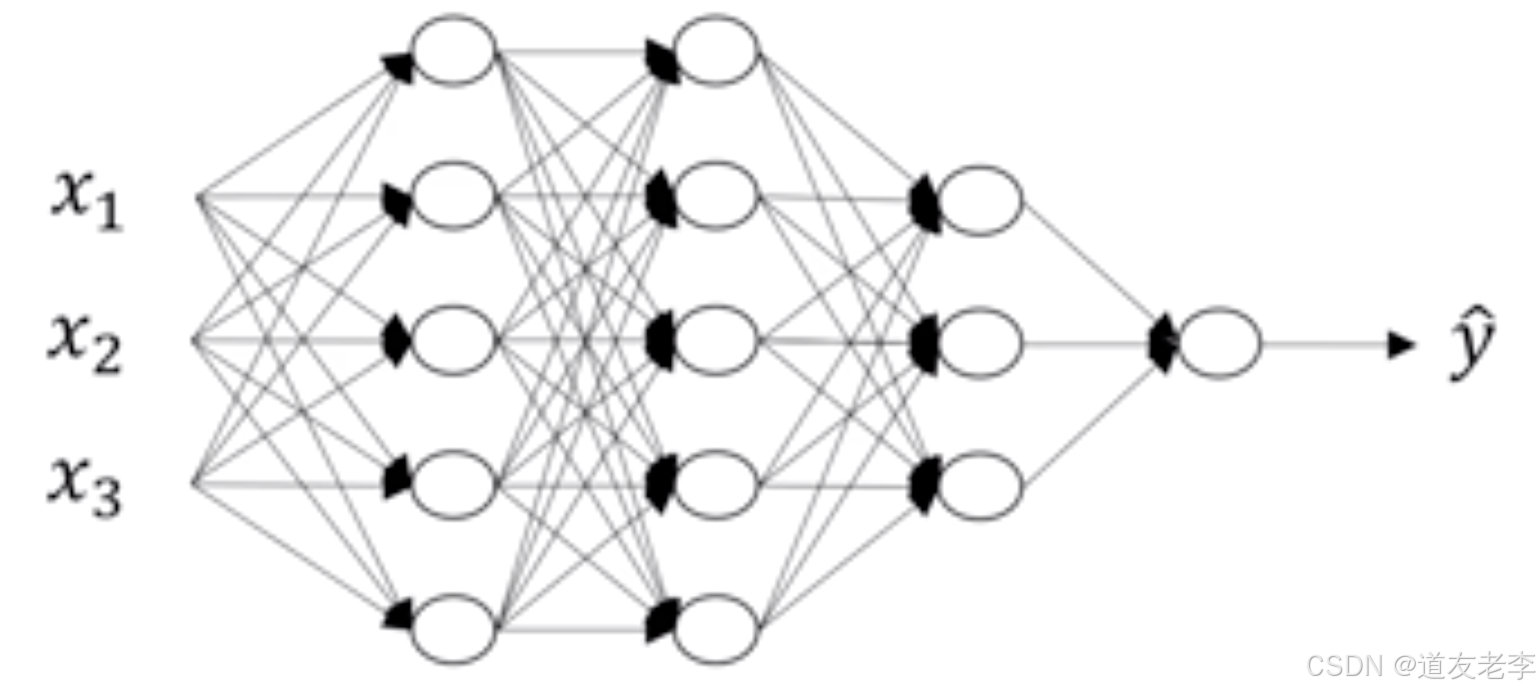
在这里首先对每层的符号进行一个确定，我们设置L为第几层，n为每一层的个数，L=[L1,L2,L3,L4],n=[5,5,3,1]

1.4.2.1 前向传播

首先还是以单个样本来进行表示,每层经过线性计算和激活函数两步计算

$z^{[1]}=W^{[1]}x+b^{[1]},a^{[1]}=g^{[1]}(z^{[1]})$, 输入$x$$,输出$$a^{[1]}$

$z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]},a^{[2]}=g^{[2]}(z^{[2]})$,输入$a^{[1]}$, 输出$a^{[2]}$

$z^{[3]}=W^{[3]}{a}^{[2]}+b^{[3]},a^{[3]}=g^{[3]}(z^{[3]})$, 输入$a^{[2]}$, 输出$a^{[3]}$

$z^{[4]}=W^{[4]}{a}^{[3]}+b^{[4]},a^{[4]}=\sigma (z^{[4]})$, 输入$a^{[3]}$, 输出$a^{[4]}$

我们将上式简单的用通用公式表达出来，$x=a^{[0]}$

$z^{[L]}=W^{[L]}{a}^{[L-1]}+b^{[L]},a^{[L]}=g^{[L]}(z^{[L]})$, 输入$a^{[L-1]}$, 输出$a^{[L]}$

• m个样本的向量表示

$Z^{[L]}=W^{[L]}{A}^{[L-1]}+b^{[L]}$

$A^{[L]}=g^{[L]}(Z^{[L]})$

输入$a^{[L-1]}$, 输出$a^{[L]}$

1.4.2.2 反向传播

因为涉及到的层数较多，所以我们通过一个图来表示反向的过程

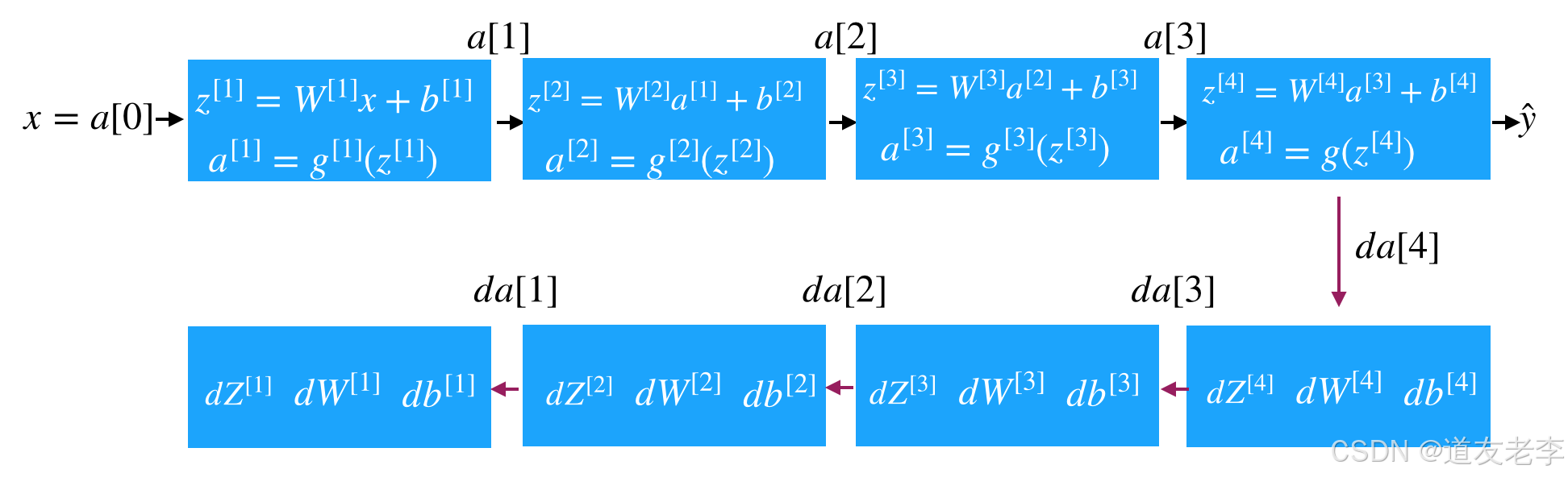
• 反向传播的结果（理解）

单个样本的反向传播：

$d{Z}^{[l]}=\frac{dJ}{d{a}^{[l]}}\frac{d{a}^{[l]}}{d{Z}^{[l]}}=d{a}^{[l]}$

$d{W}^{[l]}=\frac{dJ}{d{Z}^{[l]}}\frac{d{Z}^{[l]}}{d{W}^{[l]}}=d{Z}^{[l]}\cdot a^{[l-1]}$

$d{b}^{[l]}=\frac{dJ}{d{Z}^{[l]}}\frac{d{Z}^{[l]}}{d{b}^{[l]}}=d{Z}^{[l]}$

$d{a}^{[l-1]}=W^{[l]T}\cdot d{Z}^{[l]}$

多个样本的反向传播

$d{Z}^{[l]}=d{A}^{[l]}\ast g^{[l]}{}^{\prime }(Z^{[l]})$

$d{W}^{[l]}=\frac{1}{m}d{Z}^{[l]}\cdot {A^{[l-1]}}^T$

$d{b}^{[l]}=\frac{1}{m}np.sum(d{Z}^{[l]},axis=1)$

$d{A}^{[l]}=W^{[l+1]T}\cdot d{Z}^{[l+1]}$

1.4.3 参数与超参数

1.4.3.1 参数

参数即是我们在过程中想要模型学习到的信息（模型自己能计算出来的），例如 W[l]W[l]，b[l]b[l]。而**超参数（hyper parameters）**即为控制参数的输出值的一些网络信息（需要人经验判断）。超参数的改变会导致最终得到的参数 W[l]，b[l] 的改变。

1.4.3.2 超参数

典型的超参数有：

• 学习速率：α
• 迭代次数：N
• 隐藏层的层数：L
• 每一层的神经元个数：n[1]，n[2]，…
• 激活函数 g(z) 的选择

当开发新应用时，预先很难准确知道超参数的最优值应该是什么。因此，通常需要尝试很多不同的值。应用深度学习领域是一个很大程度基于经验的过程。

1.4.3.3 参数初始化

• 为什么要随机初始化权重

如果在初始时将两个隐藏神经元的参数设置为相同的大小，那么两个隐藏神经元对输出单元的影响也是相同的，通过反向梯度下降去进行计算的时候，会得到同样的梯度大小，所以在经过多次迭代后，两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元，其最终的影响都是相同的，那么多个隐藏神经元就没有了意义。

在初始化的时候，W 参数要进行随机初始化，不可以设置为 0。b 因为不存在上述问题，可以设置为 0。

以 2 个输入，2 个隐藏神经元为例：

W = np.random.randn(2,2)* 0.01
b = np.zeros((2,1))

• 1
• 2

• 初始化权重的值选择

这里将 W 的值乘以 0.01（或者其他的常数值）的原因是为了使得权重 W 初始化为较小的值，这是因为使用 sigmoid 函数或者 tanh 函数作为激活函数时，W 比较小，则 Z=WX+b 所得的值趋近于 0，梯度较大，能够提高算法的更新速度。而如果 W 设置的太大的话，得到的梯度较小，训练过程因此会变得很慢。

ReLU 和 Leaky ReLU 作为激活函数时不存在这种问题，因为在大于 0 的时候，梯度均为 1。