推荐|【机器学习】Adaboost 多分类与回归

文章目录

介绍
1、Adaboost多分类算例
2、Adaboost回归算例

介绍

AdaBoost（Adaptive Boosting，自适应提升）是一种集成学习方法，最初是为了解决二分类问题而设计的，但它也可以扩展到多分类和其他任务。AdaBoost通过迭代地训练一系列弱分类器，并将它们组合成一个强分类器来提高预测性能。其核心思想是在每次迭代中增加那些被前一轮分类器错误分类样本的权重，使得后续的分类器更加关注这些“困难”样本。

AdaBoost的特点

简单高效：AdaBoost算法相对简单，易于实现且计算成本较低。
无需调参：相比于其他集成方法如随机森林或梯度提升树，AdaBoost所需的超参数较少。
抗噪性差：AdaBoost对异常值和噪声较为敏感，因为错误分类的样本会被赋予更高的权重，从而可能影响后续分类器的学习过程。
容易过拟合：当数据集中存在大量噪声时，AdaBoost可能会过度拟合训练数据，导致泛化能力下降。

扩展与变体

为了克服原始AdaBoost的一些局限性，研究者们提出了多种改进版本：

AdaBoost.M1/M2：适用于多类别分类问题。
Real AdaBoost：允许弱分类器输出连续得分而不是离散标签，从而提高了灵活性。
Gentle AdaBoost：采用了更温和的方式更新样本权重，减少了对极端值的影响。
LogitBoost：基于逻辑回归的思想，通过最小化负对数似然损失函数来进行优化。

实现库

许多机器学习库都提供了AdaBoost的实现，包括但不限于：

scikit-learn：Python中非常流行的机器学习库，支持AdaBoostClassifier和AdaBoostRegressor。
Weka：Java编写的开源数据挖掘工具，内置了AdaBoostM1算法。
R语言中的adabag包：提供了AdaBoost.M1以及其他相关算法的支持。

总之，AdaBoost以其简洁性和有效性成为了一种经典的集成学习方法，在实际应用中表现出色，尤其是在特征选择、文本分类等领域。不过，在使用AdaBoost时需要注意数据质量和预处理步骤，以避免潜在的问题。

1、Adaboost多分类算例

1.1、导包

import numpy as np
from sklearn.ensemble import AdaBoostClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import graphviz

1.2、加载数据

X,y = datasets.load_iris(return_X_y = True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state = 1024)

1.3、建模

# 多分类问题，不是+1、-1
# 类别0,1,2
ada = AdaBoostClassifier(n_estimators=3,algorithm='SAMME',learning_rate=1.0)
ada.fit(X_train,y_train) #算法，工作：从X_train---y_train寻找规律
y_ = ada.predict(X_test)
proba_ = ada.predict_proba(X_test)
accuracy = ada.score(X_test,y_test)
print('--------------------算法准确率：',accuracy)
display(y_,proba_)

1.4、第一棵树构建

# 这棵树，简单的树，树的深度：1
# Adaboosting里面都是简单的树
dot_data = tree.export_graphviz(ada[0],filled=True)
graphviz.Source(dot_data)

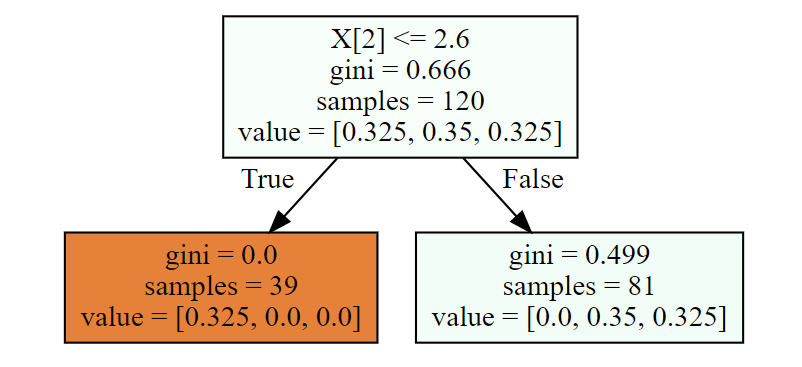
1.4.1、gini系数计算

w1 = np.full(shape = 120,fill_value=1/120)
gini = 1
for i in range(3):
    cond = y_train == i
    p = w1[cond].sum()
    gini -= p**2
print('-------------gini系数：',gini)
# 输出
'''
-------------gini系数： 0.6662499999999998
'''

1.4.2、拆分条件

best_split = {}
lower_gini = 1
# 如何划分呢，分成两部分
for col in range(X_train.shape[1]):
    for i in range(len(X_train) - 1):
        X = X_train[:,col].copy()
        X.sort()
        split = X[i:i+2].mean()
        cond = (X_train[:,col] <= split).ravel()
        part1 = y_train[cond]
        part2 = y_train[~cond]
        gini1 = 0
        gini2 = 0
        for target in np.unique(y_train):
            if part1.size != 0:
                p1 = (part1 == target).sum()/part1.size
                gini1 += p1 * (1 - p1)
            if part2.size != 0:
                p2 = (part2 == target).sum()/part2.size
                gini2 += p2 * (1 - p2)
        part1_p = w1[cond].sum()
        part2_p = 1 - part1_p
        gini  = part1_p * gini1 + part2_p* gini2
        if gini < lower_gini:
            lower_gini = gini
            best_split.clear()
            best_split['X[%d]'%(col)] = split
        elif gini == lower_gini:
            best_split['X[%d]'%(col)] = split
print(best_split)
# 输出
'''
{'X[2]': 2.5999999999999996, 'X[3]': 0.75}
'''

1.4.3、计算误差率

# 计算误差率
y1_ = ada[0].predict(X_train) #预测结果
print(y1_)
e1 = ((y_train != y1_)).mean()#误差
print('第一棵树误差率是：',e1)
print('算法的误差是：',ada.estimator_errors_)
# 输出
'''
[1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0
 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 0 1 0 0 1 1
 1 1 0 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 0 0 0 0 0 1 0 1 1 0 1 0 0
 1 1 0 1 1 1 1 1 1]
第一棵树误差率是： 0.325
算法的误差是： [0.325      0.18993352 0.1160323 ]
'''

1.4.4、计算第一个分类器权重

learning_rate = 1.0
num = 3 # 三分类
a1 = learning_rate * (np.log((1-e1)/e1) + np.log(num - 1))
print('手动计算算法权重是：',a1)

print('算法返回的分类器权重是：',ada.estimator_weights_)
# 输出
'''
手动计算算法权重是： 1.4240346891027378
算法返回的分类器权重是： [1.42403469 2.14358936 2.72369906]
'''

1.4.5、更新样本权重

# 更新样本的权重
w2 = w1 * np.exp(a1 * (y_train != y1_))
w2 /= w2.sum()
w2

1.5、第二棵树构建

# 这棵树，简单的树，树的深度：1
# Adaboosting里面都是简单的树
dot_data = tree.export_graphviz(ada[1],filled=True)
graphviz.Source(dot_data)

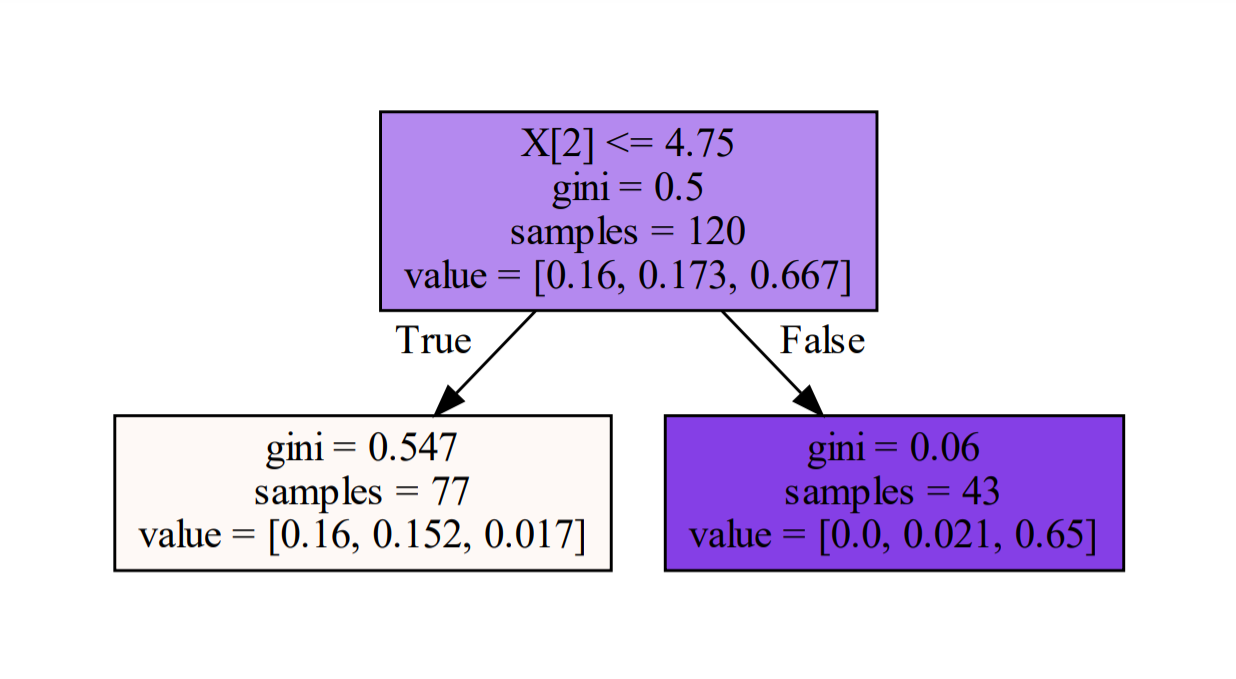
1.5.1、gini系数计算

gini = 1
for i in range(3):
    cond = y_train == i
    p = w1[cond].sum()
    gini -= p**2
print('-------------gini系数：',gini)
# 输出
'''
-------------gini系数： 0.4999237921048617
'''

1.5.2、拆分条件

best_split = {}
lower_gini = 1
# 如何划分呢，分成两部分
for col in range(X_train.shape[1]):
    for i in range(len(X_train) - 1):
        X = X_train[:,col].copy()
        X.sort()
        split = X[i:i+2].mean()
        cond = (X_train[:,col] < split).ravel()
        part1 = y_train[cond]
        part1_w2 = w2[cond]/w2[cond].sum()
        part2 = y_train[~cond]
        part2_w2 = w2[~cond]/w2[~cond].sum()
        gini1 = 1
        gini2 = 1
        for target in np.unique(y_train):
            cond1 = part1 == target
            p1 = part1_w2[cond1].sum()
            gini1 -= p1**2
            cond2 = part2 == target
            p2 = part2_w2[cond2].sum()
            gini2 -= p2**2
        part1_p = w2[cond].sum()
        part2_p = 1 - part1_p

        gini  = part1_p * gini1 + part2_p * gini2
  
        if gini < lower_gini:
            lower_gini = gini
            best_split.clear()
            best_split['X[%d]'%(col)] = split
print(best_split)
'''
{'X[2]': 4.75}
'''

1.5.3、计算误差率

# 误差
y2_ = ada[1].predict(X_train)#y2_第二个弱学习器预测值，y_train真实
e2 = ((y2_ != y_train) * w2).sum()
print('---------------第二棵树误差是：',e2)
print('算法返回每棵树的误差值是：',ada.estimator_errors_)
# 输出
'''
---------------第二棵树误差是： 0.18993352326685659
算法返回每棵树的误差值是： [0.325      0.18993352 0.1160323 ]
'''

1.5.4、计算第二个弱分类器权重

# 第二个弱学习器的权重，扁鹊医院大夫的话语权
a2 = learning_rate * (np.log((1-e2)/e2) + np.log(num - 1))
print('第二个弱分类器权重：',a2)
print('算法返回每棵树的权重是：',ada.estimator_weights_)
# 输出
'''
第二个弱分类器权重： 2.1435893615035875
算法返回每棵树的权重是： [1.42403469 2.14358936 2.72369906]
'''

1.5.5、更新样本权重

# 更新样本的权重
w3 = w2 * np.exp(a2 * (y_train != y2_))
w3 /= w3.sum()#归一化 Normalization

1.6、第三棵树构建

# 这棵树，简单的树，树的深度：1
# Adaboosting里面都是简单的树
dot_data = tree.export_graphviz(ada[2],filled=True)
graphviz.Source(dot_data)

1.6.1、gini系数计算

gini = 1
for i in range(3):
    cond = y_train == i
    p = w3[cond].sum()
    gini -= p**2
print('-------------gini系数：',gini)
# 输出
'''
-------------gini系数： 0.5204740911365549
'''

1.6.2、拆分条件

best_split = {}
lower_gini = 1
# 如何划分呢，分成两部分
for col in range(X_train.shape[1]):
    for i in range(len(X_train) - 1):
        X = X_train[:,col].copy()
        X.sort()
        split = X[i:i+2].mean()
        cond = (X_train[:,col] < split).ravel()
        part1 = y_train[cond]
        part1_w3 = w3[cond]/w3[cond].sum()
        part2 = y_train[~cond]
        part2_w3 = w3[~cond]/w3[~cond].sum()
        gini1 = 1
        gini2 = 1
        for target in np.unique(y_train):
            cond1 = part1 == target
            p1 = part1_w3[cond1].sum()
            gini1 -= p1**2
            cond2 = part2 == target
            p2 = part2_w3[cond2].sum()
            gini2 -= p2**2
        part1_p = w3[cond].sum()
        part2_p = 1 - part1_p

        gini  = part1_p * gini1 + part2_p * gini2
        if gini < lower_gini:
            lower_gini = gini
            best_split.clear()
            best_split['X[%d]'%(col)] = split
print(best_split)
'''
{'X[3]': 1.65}
'''

1.6.3、计算误差率

# 误差
y3_ = ada[2].predict(X_train)#y3_表示第三个弱学习器预测值，y_train真实
e3 = ((y3_ != y_train)* w3).sum()
print('---------------',e3)
print('算法返回每棵树的误差值是：',ada.estimator_errors_)
# 输出
'''
--------------- 0.11603230428552824
算法返回每棵树的误差值是： [0.325      0.18993352 0.1160323 ]
'''

1.6.4、计算第三个弱分类器权重

# 第三个弱学习器的权重，扁鹊医院大夫的话语权
a3 = learning_rate*(np.log((1-e3)/e3) + np.log(num - 1))
print('第三个弱分类器权重：',a3)
print('算法返回每棵树的权重是：',ada.estimator_weights_)
# 输出
'''
第三个弱分类器权重： 2.72369906166382
算法返回每棵树的权重是： [1.42403469 2.14358936 2.72369906]
'''

1.7、概率计算

1.7.1、算法预测

y_ = ada.predict(X_test)
proba_ = ada.predict_proba(X_test)#Adaboosting算法，概率问题
display(y_,proba_[:5])
# 输出
'''
array([1, 0, 2, 2, 0, 0, 1, 2, 1, 0, 0, 0, 1, 2, 1, 0, 1, 0, 1, 0, 2, 0,
       1, 0, 2, 1, 2, 2, 2, 2])
array([[0.33156225, 0.38881125, 0.2796265 ],
       [0.3719898 , 0.34785853, 0.28015167],
       [0.2783866 , 0.31174493, 0.40986847],
       [0.2783866 , 0.31174493, 0.40986847],
       [0.3719898 , 0.34785853, 0.28015167]])
'''

1.7.2、代码实现概率预测

# numpy运算，功能特别强大！！！
y1_ = (ada[0].predict(X_test) == np.array([[0],[1],[2]])).T.astype(np.int8)
y2_ = (ada[1].predict(X_test) == np.array([[0],[1],[2]])).T.astype(np.int8)
y3_ = (ada[2].predict(X_test) == np.array([[0],[1],[2]])).T.astype(np.int8)

# 根据权重将弱分类器组合
pred = y1_ * a1 + y2_ * a2 + y3_ * a3
pred/=estimator_weights.sum()
pred/=(num -1)
proba = np.e**pred/((np.e**pred).sum(axis = 1).reshape(-1,1))
proba[:5]
# 输出
'''
array([[0.33156225, 0.38881125, 0.2796265 ],
       [0.3719898 , 0.34785853, 0.28015167],
       [0.2783866 , 0.31174493, 0.40986847],
       [0.2783866 , 0.31174493, 0.40986847],
       [0.3719898 , 0.34785853, 0.28015167]])
'''

2、Adaboost回归算例

2.1、加载数据

import numpy as np
from sklearn.ensemble import AdaBoostRegressor
from sklearn import datasets
from sklearn import tree
import graphviz

X,y = datasets.load_boston(return_X_y=True)

2.2、建模

ada = AdaBoostRegressor(n_estimators=3,loss = 'linear',# 线性，误差绝对值
                                 learning_rate=1)#learning_rate 学习率
ada.fit(X,y)#训练
y_ = ada.predict(X)#预测
print(y_[:10])

2.3、模型可视化

dot_data = tree.export_graphviz(ada[0],filled=True)
graph = graphviz.Source(dot_data)
graph

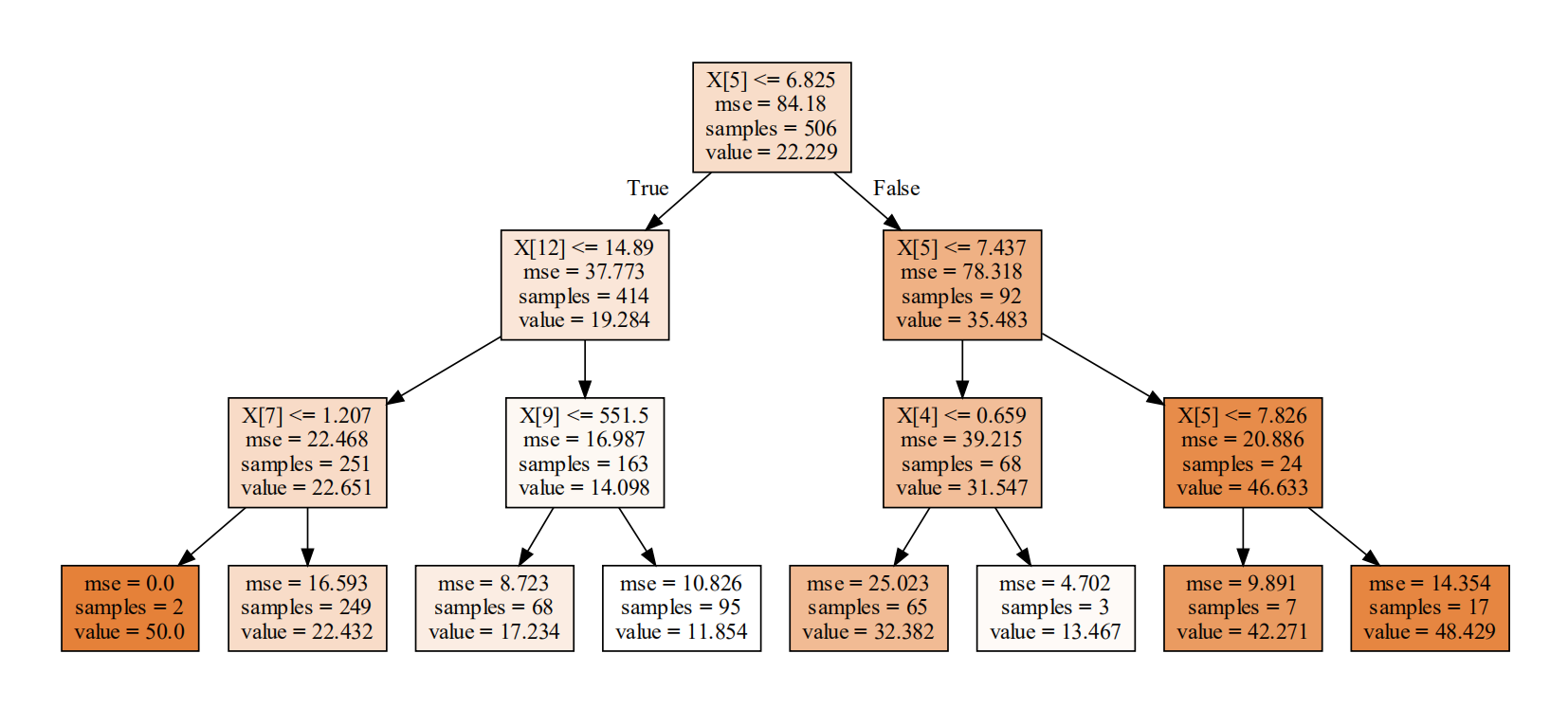
2.4、回归树算法流程

1、初始权重，所有样本权重一样都是 $\frac{1}{m}$ ， m表示样本数量

$w_{(1)} = [w_{11},w_{12},…w_{1m}],w_{1i} = \frac{1}{m},i = 1,2,…,m$

2、接下来，进行for循环遍历k = 1,2,3,…k，表示k棵树

a) 使用具有权重

$w_{(k)}$ 的样本集来训练数据，得到弱学习器 $G_k(x)$

b) 计算训练集上的最大误差

$E_k = max|y_i - G_k(x_i)|,i = 1,2,…,m$

c) 计算每个样本的相对误差

如果是线性误差，则：

$e_{ki} = \frac{|y_i - G_k(x_i)|}{E_k}$

如果是平方误差，则：

$e_{ki} = \frac{(y_i - G_k(x_i))^2}{E_k^2}$

如果是指数误差，则：

$e_{ki} = 1 - exp({-\frac{|y_i - G_k(x_i)|}{E_k}})$

d) 计算回归误差率

$e_k = \sum\limits_{i = 1}^mw_{ki}e_{ki}$

e) 计算弱学习器的权重

$\frac{e_k}{1 - e_k}$

$\alpha_k = ln\frac{1}{beta}$

f) 更新样本权重分布

$w_{(k + 1)i} = w_{ki} \times beta^{1 - e_{ki}}$

$w_{(k + 1)i} = w_{(k + 1)i} / \sum\limits_{i=1}^mw_{(k+1)i}$

2.4、第一棵树构建

w1 = np.full(shape = 506,fill_value=1/506)
y1_ = ada[0].predict(X)

# 计算预测值和目标值的误差
error_vector = np.abs(y1_ - y)
error_max = error_vector.max()
if error_max != 0:
    error_vector /= error_max # 归一化0~1

# 计算算法误差
estimator_error = (w1 * error_vector).sum()
print('第一棵树误差：',estimator_error)
print('算法误差：',ada.estimator_errors_)

# 计算算法权重
beta = estimator_error / (1. - estimator_error)
estimator_weight =  np.log(1. / beta)
print('第一棵树权重：',estimator_weight)
print('算法权重：', ada.estimator_weights_)

# 根据第一棵树更新权重
w2 = w1 * np.power(beta, (1. - error_vector))
w2 /= w2.sum()
# 输出
'''
第一棵树误差： 0.11315306016068988
算法误差： [0.11315306 0.11657419 0.18593167]
第一棵树权重： 2.0589309911688427
算法权重： [2.05893099 2.02527945 1.47666508]
'''

2.5、第二棵树构建

y2_ = ada[1].predict(X)

# 计算预测值和目标值的误差
error_vector = np.abs(y2_ - y)
error_max = error_vector.max()
if error_max != 0:
    error_vector /= error_max # 归一化

# 计算算法误差
estimator_error = (w2 * error_vector).sum()
print('第二棵树误差：',estimator_error)
print('算法误差：',ada.estimator_errors_)

# 计算算法权重
beta = estimator_error / (1. - estimator_error)
estimator_weight =  np.log(1. / beta)
print('第二棵树权重：',estimator_weight)
print('算法权重：', ada.estimator_weights_)

# 权重更新
w3 = w2 * np.power(beta, (1. - error_vector))
w3 /= w3.sum()
# 输出
'''
第二棵树误差： 0.11657418722530435
算法误差： [0.11315306 0.11657419 0.18593167]
第二棵树权重： 2.0252794479876193
算法权重： [2.05893099 2.02527945 1.47666508]
'''

2.6、第三棵树构建

y3_ = ada[2].predict(X)

# 计算预测值和目标值的误差
error_vector = np.abs(y3_ - y)
error_max = error_vector.max()
if error_max != 0:
    error_vector /= error_max

# 计算算法误差
estimator_error = (w3 * error_vector).sum()
print('第三棵树误差：',estimator_error)
print('算法误差：',ada.estimator_errors_)

# 计算算法权重
beta = estimator_error / (1. - estimator_error)
estimator_weight =  np.log(1. / beta)
print('第三棵树权重：',estimator_weight)
print('算法权重：', ada.estimator_weights_)
# 输出
'''
第三棵树误差： 0.1859316681718044
算法误差： [0.11315306 0.11657419 0.18593167]
第三棵树权重： 1.4766650774202654
算法权重： [2.05893099 2.02527945 1.47666508]
'''