【机器学习】KNN近邻算法及实战案例（鸢尾花、手写数字识别）

文章目录

1、KNN介绍

K-Nearest Neighbors (KNN) 是一种简单且直观的机器学习算法，它属于监督学习的一种。KNN可以用于分类和回归问题，但最常用于分类。它的核心思想是：一个样本所属的类别可以通过与这个样本最近邻的几个训练样本的类别来决定。

KNN的工作原理

  • 选择距离度量方法：
    • 为了找到最近邻居，首先需要定义“近”的标准，即如何衡量两个样本之间的距离。常用的距离度量包括欧氏距离、曼哈顿距离等。
  • 确定邻居数量（k值）：
    • k值决定了考虑多少个最近邻。较小的k值意味着模型更复杂，容易过拟合；较大的k值则可能包含更多的噪声，导致欠拟合。选择合适的k值是一个重要的参数调整过程。
  • 寻找k个最近邻：
    • 对于每一个测试样本，计算它与所有训练样本之间的距离，并选出距离最近的k个训练样本作为其邻居。
  • 决策规则：
    • 在分类任务中，多数表决法则被用来确定新样本的类别，即新样本将被分配给其k个邻居中最常见的类别。
    • 在回归任务中，通常会取这k个邻居的目标变量值的平均值作为预测结果。

KNN的特点

  • 非参数化：KNN不需要对数据分布做任何假设，因此它是非参数化的。
  • 懒惰学习：KNN是一种懒惰学习算法，因为它在训练阶段不做太多工作，只是存储训练数据。所有的计算都发生在预测阶段。
  • 计算成本高：由于每次预测都需要遍历整个训练集以计算距离，所以对于大型数据集，KNN可能会变得非常慢。
  • 对特征尺度敏感：如果不同特征有不同的量级范围，那么具有较大数值范围的特征将会主导距离计算。因此，在应用KNN之前，最好先进行特征缩放（如标准化或归一化）。
  • 受维数灾难影响：随着特征数量增加，样本点之间的距离差异减小，使得最近邻的选择变得更加困难。这就是所谓的“维数灾难”。

优点

  • 简单易懂，实现起来相对容易。
  • 可以处理多分类问题。
  • 不需要复杂的训练过程。

缺点

  • 预测速度慢，尤其是在大数据集上。
  • 对异常值敏感。
  • 参数k的选择对模型性能有很大影响。
  • 如果特征空间维度很高，则效果不佳。

应用场景

KNN适用于那些有清晰边界的数据集，特别是当数据集不是特别大时。它也被广泛应用于推荐系统、图像识别等领域。

1.1、什么是KNN

  • k nearest neighbors

  • k近邻算法

  • k表示个数

    • 你有几个好朋友？
    • 你有几个邻居？
    • 你有几个女朋友？

  • 邻居是什么样性质，类别，影响你，之所以成为了邻居，必然共性

  • 根据这个特征，来对事物进行分类

1.2、KNN过程实现

  • 邻居，距离比较近

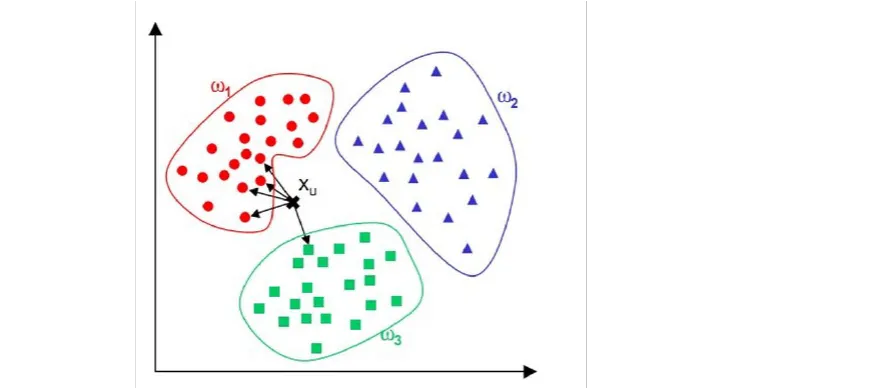
  • image.png

    • 问题，请问Xu这个点属于哪个类别呢？
    • 三个类别：红色、绿色、蓝色
    • 找Xu这个点的最近的5个邻居（5 == k，调大跳小）
    • 从图中直观看到，4个最近邻居是红色，1个最近的邻居是绿色
    • 人多力量大，投票决定，民主。4 > 1
    • 对人而言，投票
    • 对计算机而言，统计
    • 0.8 > 0.2
    • 从票数或者从概率上分类的话，得到这样的结论
    • Xu属于红色的类别！
    • KNN根据远近，进行类别划分的基本原理

1.3、距离度量

  • 距离

  • 点A(1,2)，点B(4,6)，请问A和B之间的距离怎么计算

  • 欧式距离

  • d i s t a n c e A B = ( 4 − 1 ) 2 + ( 6 − 2 ) 2 = 3 2 + 4 2 = 5 distance_{AB} = \sqrt{(4 - 1)^2 + (6-2)^2} = \sqrt{3^2 + 4^2} = 5 distanceAB​=(4−1)2+(6−2)2 ​=32+42 ​=5

  • 点A(2,3,4)，点B(5,8,9):

  • d i s t a n c e A B = ( 5 − 2 ) 2 + ( 8 − 3 ) 2 + ( 9 − 4 ) 2 distance_{AB} = \sqrt{(5-2)^2 + (8-3)^2 + (9-4)^2} distanceAB​=(5−2)2+(8−3)2+(9−4)2 ​

  • 点A(x1,x2,x3,x4,……xn)，B(y1,y2,y3,y4,……yn)：

  • d i s t a n c e A B = ∑ i = 1 n ( x i − y i ) 2 distance_{AB} = \sqrt{\sum_{i=1}^n(x_i - y_i)^2} distanceAB​=i=1∑n​(xi​−yi​)2 ​

  • 上面这个公式就是欧几里得距离公式

  • KNN算法的理论基础就是：

    • 欧式距离
    • 根据距离远近，选择邻居
    • 物以类聚人以群分
    • 这个算法不难！

1.4、KNN算法缺陷

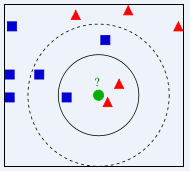
image.png

  • k给多少比较好呢？
  • 请问绿色的点划归到红色类别，还是蓝色的类别？
  • 如果k = 3，找三个邻居，2个是红色，1个蓝色 投票，红色票数多，所以此时，绿色球划归到，红色的类别
  • 如果k = 5，找五个邻居，3个是蓝色，2个红色 投票，蓝色票数多，所以此时，绿色球划归到，蓝色的类别
  • 分歧，不一致，不稳定，给定的k值不同，结果可能会不同！

1.5、KNN总结

  • KNN算法怎么找到邻居的呢？

    • 电脑而言，给了一堆数据
    • 电脑，计算所有点的距离！
    • 然后排序！
    • 选择距离比较小的k个点！
    • 穷举
    • KNN算法，比较耗费时间，要求数据量不能太大，时间复杂度空间复杂度，比较大。

  • KNN这个算法，比较简单，但是，很多情况下，比较实用的。

    • 数据，都是存在规律，精确度要求不高，KNN这个算法，可以实现分类功能。

2、KNN的案例

  • 鸢尾花分类
  • 生长的环境不同，所以类别3类
  • 类别不同，性质不同：花萼长宽不一样，花瓣长宽不同了。
  • 植物学家，根据形状不同，进行分类
  • 分类算法使用流程：
    • 加载数据
    • 数据预处理，拆分
    • 声明算法，给定超参数
    • 训练算法，算法学习数据，归纳规律
    • 算法，通过数学，找到，数据和目标值之间的规律
    • 算法找到规律，应用
    • 实际使用了。

3、KNN超参数

  • 邻居
  • weights权重，话语权：uniform、distance
  • p = 1、2
  • metrics = minkowski
  • p = 1 曼哈顿距离
    • 这个距离表示远近方法
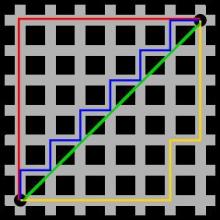
    • image.png
    • 红色的线就是曼哈顿距离
    • 蓝色和黄色等价曼哈顿距离
    • 绿色线就是欧式距离
  • p = 2 欧式距离

4、手写数字识别【实战案例】

  • 数据加载
  • 数据转换
  • 数据清洗
  • 算法建模
  • 算法预测
  • 数据可视化

5、癌症诊断【实战案例】

  • 有一些微观数据，都是人体细胞内的数据
  • 中医：望闻问切
  • 西医：各种设备，检查一通
  • 无论中医还是西医：
    • 获取指标
    • 获取数据
    • 获取特征
  • 看病，通过，指标诊断
  • 设备越来越先进，获取更多微观数据、指标
  • 有一些病，先微观，变成宏观（感觉不舒服）
  • 量变到质变
  • 可以尝试找到围观数据和疾病之间的关系！
  • 使用算法寻找数据内部的规律
  • KNN调整超参数，准确率提升
  • 数据归一化、标准化，提升更加明显！

6、薪资预测【实战案例】

  • 属性清理，将没用属性删除
  • 一些属性是str类型的
  • pandas中map、agg、apply、transform这些都可以转变！
  • 建模
    • knn
    • knn.fit()
    • knn.predict()预测
    • knn.score()准确率，分类
  • 模型优秀，模型准确率更高
    • 超参数调整
    • 归一化、标准化
    • pandas.cut()，分箱操作，面元化操作，其实就是分类
    • 把相近的数值，归到一类中
    • 大学时候，体育成绩：优（90～100）、良（80～90）、中等（70～80）、及格（60～70）、不及格（<60）
    • 大学成绩，就是分箱操作。
    • 简明扼要。

实战案例

鸢尾花Iris

数据加载

from sklearn.neighbors import KNeighborsClassifier # 根据邻居，进行分类
from sklearn import datasets # 方便学习，为我们提供的数据

# X大写，约定
X,y = datasets.load_iris(return_X_y=True)# 鸢尾花，分三类，鸢尾花花萼和花瓣长宽
display(X,y)

from sklearn.model_selection import train_test_split # 数据进行拆分
# train训练数据，将训练数据，交给算法，进行建模，总结规律
# test测试，应用规律
# train_test_split拆分数据【随机拆分】
# 因为随机，X_train和X_test每次，结果会不同！
# 难题，简单
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=11) # 30个测试数据
display(X_train.shape,X_test.shape)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       [5.4, 3.9, 1.7, 0.4],
       [4.6, 3.4, 1.4, 0.3],
       [5. , 3.4, 1.5, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.1],
       [5.4, 3.7, 1.5, 0.2],
       [4.8, 3.4, 1.6, 0.2],
       [4.8, 3. , 1.4, 0.1],
       [4.3, 3. , 1.1, 0.1],
       [5.8, 4. , 1.2, 0.2],
       [5.7, 4.4, 1.5, 0.4],
       [5.4, 3.9, 1.3, 0.4],
       [5.1, 3.5, 1.4, 0.3],
       [5.7, 3.8, 1.7, 0.3],
       [5.1, 3.8, 1.5, 0.3],
       [5.4, 3.4, 1.7, 0.2],
       [5.1, 3.7, 1.5, 0.4],
       [4.6, 3.6, 1. , 0.2],
       [5.1, 3.3, 1.7, 0.5],
       [4.8, 3.4, 1.9, 0.2],
       [5. , 3. , 1.6, 0.2],
       [5. , 3.4, 1.6, 0.4],
       [5.2, 3.5, 1.5, 0.2],
       [5.2, 3.4, 1.4, 0.2],
       [4.7, 3.2, 1.6, 0.2],
       [4.8, 3.1, 1.6, 0.2],
       [5.4, 3.4, 1.5, 0.4],
       [5.2, 4.1, 1.5, 0.1],
       [5.5, 4.2, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.2],
       [5. , 3.2, 1.2, 0.2],
       [5.5, 3.5, 1.3, 0.2],
       [4.9, 3.6, 1.4, 0.1],
       [4.4, 3. , 1.3, 0.2],
       [5.1, 3.4, 1.5, 0.2],
       [5. , 3.5, 1.3, 0.3],
       [4.5, 2.3, 1.3, 0.3],
       [4.4, 3.2, 1.3, 0.2],
       [5. , 3.5, 1.6, 0.6],
       [5.1, 3.8, 1.9, 0.4],
       [4.8, 3. , 1.4, 0.3],
       [5.1, 3.8, 1.6, 0.2],
       [4.6, 3.2, 1.4, 0.2],
       [5.3, 3.7, 1.5, 0.2],
       [5. , 3.3, 1.4, 0.2],
       [7. , 3.2, 4.7, 1.4],
       [6.4, 3.2, 4.5, 1.5],
       [6.9, 3.1, 4.9, 1.5],
       [5.5, 2.3, 4. , 1.3],
       [6.5, 2.8, 4.6, 1.5],
       [5.7, 2.8, 4.5, 1.3],
       [6.3, 3.3, 4.7, 1.6],
       [4.9, 2.4, 3.3, 1. ],
       [6.6, 2.9, 4.6, 1.3],
       [5.2, 2.7, 3.9, 1.4],
       [5. , 2. , 3.5, 1. ],
       [5.9, 3. , 4.2, 1.5],
       [6. , 2.2, 4. , 1. ],
       [6.1, 2.9, 4.7, 1.4],
       [5.6, 2.9, 3.6, 1.3],
       [6.7, 3.1, 4.4, 1.4],
       [5.6, 3. , 4.5, 1.5],
       [5.8, 2.7, 4.1, 1. ],
       [6.2, 2.2, 4.5, 1.5],
       [5.6, 2.5, 3.9, 1.1],
       [5.9, 3.2, 4.8, 1.8],
       [6.1, 2.8, 4. , 1.3],
       [6.3, 2.5, 4.9, 1.5],
       [6.1, 2.8, 4.7, 1.2],
       [6.4, 2.9, 4.3, 1.3],
       [6.6, 3. , 4.4, 1.4],
       [6.8, 2.8, 4.8, 1.4],
       [6.7, 3. , 5. , 1.7],
       [6. , 2.9, 4.5, 1.5],
       [5.7, 2.6, 3.5, 1. ],
       [5.5, 2.4, 3.8, 1.1],
       [5.5, 2.4, 3.7, 1. ],
       [5.8, 2.7, 3.9, 1.2],
       [6. , 2.7, 5.1, 1.6],
       [5.4, 3. , 4.5, 1.5],
       [6. , 3.4, 4.5, 1.6],
       [6.7, 3.1, 4.7, 1.5],
       [6.3, 2.3, 4.4, 1.3],
       [5.6, 3. , 4.1, 1.3],
       [5.5, 2.5, 4. , 1.3],
       [5.5, 2.6, 4.4, 1.2],
       [6.1, 3. , 4.6, 1.4],
       [5.8, 2.6, 4. , 1.2],
       [5. , 2.3, 3.3, 1. ],
       [5.6, 2.7, 4.2, 1.3],
       [5.7, 3. , 4.2, 1.2],
       [5.7, 2.9, 4.2, 1.3],
       [6.2, 2.9, 4.3, 1.3],
       [5.1, 2.5, 3. , 1.1],
       [5.7, 2.8, 4.1, 1.3],
       [6.3, 3.3, 6. , 2.5],
       [5.8, 2.7, 5.1, 1.9],
       [7.1, 3. , 5.9, 2.1],
       [6.3, 2.9, 5.6, 1.8],
       [6.5, 3. , 5.8, 2.2],
       [7.6, 3. , 6.6, 2.1],
       [4.9, 2.5, 4.5, 1.7],
       [7.3, 2.9, 6.3, 1.8],
       [6.7, 2.5, 5.8, 1.8],
       [7.2, 3.6, 6.1, 2.5],
       [6.5, 3.2, 5.1, 2. ],
       [6.4, 2.7, 5.3, 1.9],
       [6.8, 3. , 5.5, 2.1],
       [5.7, 2.5, 5. , 2. ],
       [5.8, 2.8, 5.1, 2.4],
       [6.4, 3.2, 5.3, 2.3],
       [6.5, 3. , 5.5, 1.8],
       [7.7, 3.8, 6.7, 2.2],
       [7.7, 2.6, 6.9, 2.3],
       [6. , 2.2, 5. , 1.5],
       [6.9, 3.2, 5.7, 2.3],
       [5.6, 2.8, 4.9, 2. ],
       [7.7, 2.8, 6.7, 2. ],
       [6.3, 2.7, 4.9, 1.8],
       [6.7, 3.3, 5.7, 2.1],
       [7.2, 3.2, 6. , 1.8],
       [6.2, 2.8, 4.8, 1.8],
       [6.1, 3. , 4.9, 1.8],
       [6.4, 2.8, 5.6, 2.1],
       [7.2, 3. , 5.8, 1.6],
       [7.4, 2.8, 6.1, 1.9],
       [7.9, 3.8, 6.4, 2. ],
       [6.4, 2.8, 5.6, 2.2],
       [6.3, 2.8, 5.1, 1.5],
       [6.1, 2.6, 5.6, 1.4],
       [7.7, 3. , 6.1, 2.3],
       [6.3, 3.4, 5.6, 2.4],
       [6.4, 3.1, 5.5, 1.8],
       [6. , 3. , 4.8, 1.8],
       [6.9, 3.1, 5.4, 2.1],
       [6.7, 3.1, 5.6, 2.4],
       [6.9, 3.1, 5.1, 2.3],
       [5.8, 2.7, 5.1, 1.9],
       [6.8, 3.2, 5.9, 2.3],
       [6.7, 3.3, 5.7, 2.5],
       [6.7, 3. , 5.2, 2.3],
       [6.3, 2.5, 5. , 1.9],
       [6.5, 3. , 5.2, 2. ],
       [6.2, 3.4, 5.4, 2.3],
       [5.9, 3. , 5.1, 1.8]])



array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])



(120, 4)



(30, 4)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168

算法建模

# 新的，里面没有内容
knn = KNeighborsClassifier(n_neighbors=5)

# 120个鸢尾花的特征数据和目标值，对应关系
# 这里的fit，就是向里面填充内容
# 没有fit这一步，下面都不能执行
knn.fit(X_train,y_train)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
KNeighborsClassifier()
  • 1

算法验证

# 预测结果，y_一般情况下，字母后面带_，表示算法结果
y_ = knn.predict(X_test)
# y_test表示真实答案【有真实答案】
display(y_test,y_)
  • 1
  • 2
  • 3
  • 4
array([2, 2, 2, 1, 2, 0, 1, 0, 0, 1, 2, 1, 1, 2, 2, 0, 2, 1, 2, 2, 1, 0,
       0, 1, 0, 0, 2, 1, 0, 1])



array([2, 2, 2, 1, 2, 0, 1, 0, 0, 1, 1, 1, 1, 2, 2, 0, 2, 1, 2, 2, 1, 0,
       0, 1, 0, 0, 2, 1, 0, 1])
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
type(knn) # 类，里面包含，规律，
  • 1
sklearn.neighbors._classification.KNeighborsClassifier
  • 1
knn.score(X_test,y_test)
  • 1
0.9666666666666667
  • 1
(y_test == y_).mean()
  • 1
0.9666666666666667
  • 1

算法应用

# 应用，新数据【应用】
# 从野外采集新的数据，手机在野外，拍照，照片传到服务器
# 服务器进行计算，鸢尾花特征，进行类别判别
# 人员，采集鸢尾花，数据，算法批量的判别类型
  • 1
  • 2
  • 3
  • 4

模型保存

pip install joblib
  • 1
Looking in indexes: https://mirrors.aliyun.com/pypi/simple
Requirement already satisfied: joblib in d:\soft\python\396\lib\site-packages (1.1.0)
Note: you may need to restart the kernel to use updated packages.


WARNING: You are using pip version 21.1.3; however, version 22.1 is available.
You should consider upgrading via the 'd:\soft\python\396\python.exe -m pip install --upgrade pip' command.
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
import joblib # job工作，lib图书馆
  • 1
joblib.dump(knn,'./model')
  • 1
['./model']
  • 1
model = joblib.load('./model')
type(model)
  • 1
  • 2
sklearn.neighbors._classification.KNeighborsClassifier
  • 1
model.score(X_test,y_test)
  • 1
0.9666666666666667
  • 1
import numpy as np
# 我随机给的一个试验数据
X_new = np.array([[5.4,3.2,0.8,2.3]])
model.predict(X_new) # 判定，这个数据对应鸢尾花类别0
  • 1
  • 2
  • 3
  • 4
array([0])
  • 1

超参数

import matplotlib.pyplot as plt
knn = KNeighborsClassifier() # 可以在构造方法中，进行设置
scores = []
for k in range(2,50):
    knn.set_params(n_neighbors = k) # 重新设置参数的意思
    knn.fit(X_train,y_train)
    score = knn.score(X_test,y_test)
    scores.append(score)
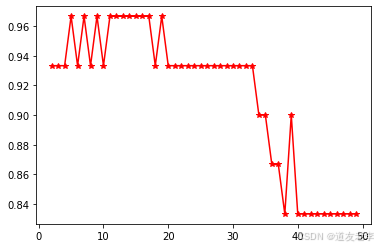
# 不同K值，对，准确率影响
# K选择：5、7、9（尽量，奇数）
# 选择5个邻居，可以了
# 选择5个，就行
# 选择6时（偶数），不好，投票（平局）
plt.plot(np.arange(2,50),scores,'*r-')
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
[]
  • 1

在这里插入图片描述

knn = KNeighborsClassifier(n_neighbors=5, weights='distance')
knn.fit(X_train,y_train)
knn.score(X_test,y_test)
  • 1
  • 2
  • 3
0.9666666666666667
  • 1
knn = KNeighborsClassifier(n_neighbors=5, weights='uniform')# 统一，制服
knn.fit(X_train,y_train)
knn.score(X_test,y_test)
  • 1
  • 2
  • 3
0.9666666666666667
  • 1
knn = KNeighborsClassifier(n_neighbors=5, weights='distance',p = 1)
knn.fit(X_train,y_train)
knn.score(X_test,y_test)
  • 1
  • 2
  • 3
0.9333333333333333
  • 1
knn = KNeighborsClassifier(n_neighbors=5, weights='distance',p = 2)
knn.fit(X_train,y_train)
knn.score(X_test,y_test)
  • 1
  • 2
  • 3
0.9666666666666667
  • 1

手写数字识别

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier

from sklearn.model_selection import train_test_split
  • 1
  • 2
  • 3
  • 4
  • 5

数据加载

data = np.load('./digit.npy')
# 5000个手写数字
# 每个手写数字：高度是28像素，宽度是28像素
# 0~499数字0
# 500~999数字1
# 最后500个是数字9
data.shape
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
(5000, 28, 28)
  • 1
index = np.random.randint(0,5000,size = 1)[0]
print(index)
plt.figure(figsize=(2,2))
plt.imshow(data[index])
  • 1
  • 2
  • 3
  • 4
2122
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7

在这里插入图片描述

# 创建目标值
y = np.array([0,1,2,3,4,5,6,7,8,9]*500)
y = np.sort(y)# 前500个是0，后500个是9
  • 1
  • 2
  • 3

数据拆分

data = data.reshape(5000,-1)
# 784表示样本每一个像素
# 图片，之所以，看到的数字不同，本质上，是像素不同
# 相随，作为特征，来进行训练
data.shape
  • 1
  • 2
  • 3
  • 4
  • 5
(5000, 784)
  • 1
# 经过上面的处理，data ---> y【一一对应】
X_train,X_test,y_train,y_test = train_test_split(data,y,test_size=0.1) #保留 500个数据作为验证数据
display(X_train.shape,X_test.shape)
  • 1
  • 2
  • 3
(4500, 784)



(500, 784)
  • 1
  • 2
  • 3
  • 4
  • 5

算法建模

X_train.ndim
  • 1
2
  • 1
knn = KNeighborsClassifier(n_neighbors=10)
# 强调：算法接收的数据，必须是二维的！！！
# 第一维是，样本数量，第二维是每个样本的特征！
knn.fit(X_train,y_train)
  • 1
  • 2
  • 3
  • 4
KNeighborsClassifier(n_neighbors=10)
  • 1

算法验证

# 预测的手写数字
y_ = knn.predict(X_test)
display(y_test[:20],y_[:20])
  • 1
  • 2
  • 3
array([3, 5, 2, 9, 6, 4, 1, 0, 8, 1, 8, 6, 7, 3, 7, 9, 6, 5, 9, 8])
array([3, 5, 2, 9, 6, 4, 1, 0, 8, 1, 8, 6, 7, 3, 7, 9, 6, 6, 9, 8])
  • 1
  • 2
knn.score(X_test,y_test)
  • 1
0.93
  • 1

可视化

# 50个
plt.figure(figsize=(2*5,3*10))
# mnist美国一个机构，花钱雇人写的
for i in range(50):
    # 10行5列
    plt.subplot(10,5,i+1)
    plt.imshow(X_test[i].reshape(28,28))
    plt.axis('off')
    plt.title('True:%d\nPredict:%d' % (y_test[i],y_[i]))
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9

在这里插入图片描述

注：本文转载自blog.csdn.net的道友老李的文章"https://blog.csdn.net/u014608435/article/details/144524819"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！