MSK接收

文章目录

前言

MSK解调 M序列相关 峰值检测 抽样判决 RS解码 等流程记录

一、MSK解调

MSK信号调制好后表达式如下所示：
S M S K ( t ) = cos ⁡ ( ω c t + π a k 2 T s t + φ k ) , ( k − 1 ) T s ≤ t ≤ k T s , k = 1 , 2 , 3 , ⋯ ⋯ S_{M S K}(t)=cos left(omega_{c} t+frac{pi a_{k}}{2 T_{s}} t+varphi_{k} ight),(k-1) T_{s} leq t leq k T_{s}, k=1,2,3, cdots cdots SMSK​(t)=cos(ωc​t+2Ts​πak​​t+φk​),(k−1)Ts​≤t≤kTs​,k=1,2,3,⋯⋯

请添加图片描述
在移动或是室内的无线通信中,由多径引起的衰落将使相干解调的性能严重下降,误码率随之上升。此时,非相干解调更为合适。同时非相干解调结构简单,不需要载波同步，也不需要频偏、相偏的估计补偿，易于实现，后续采用非相干解调。

与I路本地载波相乘得（存在相偏）：
S M S K ( t ) cos ⁡ ( ω c t + ψ ) = cos ⁡ ( ω c t + π t 2 T s a k + φ k ) cos ⁡ ( ω c t + ψ ) = 1 2 cos ⁡ ( 2 ω c t + π t 2 T s a k + φ k + ψ ) + 1 2 cos ⁡ ( π t 2 T s a k + φ k − ψ ) S_{M S K}(t) cos left(omega_{c} t+psi ight)=cos left(omega_{c} t+frac{pi t}{2 T_{s}} a_{k}+varphi_{k} ight) cos left(omega_{c} t+psi ight) \ =frac{1}{2} cos left(2 omega_{c} t+frac{pi t}{2 T_{s}} a_{k}+varphi_{k}+psi ight)+frac{1}{2} cos left(frac{pi t}{2 T_{s}} a_{k}+varphi_{k}-psi ight) SMSK​(t)cos(ωc​t+ψ)=cos(ωc​t+2Ts​πt​ak​+φk​)cos(ωc​t+ψ)=21​cos(2ωc​t+2Ts​πt​ak​+φk​+ψ)+21​cos(2Ts​πt​ak​+φk​−ψ)

请添加图片描述

与Q路本地载波相乘得（存在相偏）：
S M S K ( t ) ( − sin ⁡ ( ω c t + ψ ) ) = cos ⁡ ( ω c t + π t 2 T s a k + φ k ) ( − sin ⁡ ( ω c t + ψ ) ) = 1 2 sin ⁡ ( π t 2 T s a k + φ k − ψ ) − 1 2 sin ⁡ ( 2 ω c t + π t 2 T s a k + φ k + ψ ) S_{M S K}(t)left(-sin left(omega_{c} t+psi ight) ight)=cos left(omega_{c} t+frac{pi t}{2 T_{s}} a_{k}+varphi_{k} ight)left(-sin left(omega_{c} t+psi ight) ight) \ =frac{1}{2} sin left(frac{pi t}{2 T_{s}} a_{k}+varphi_{k}-psi ight)-frac{1}{2} sin left(2 omega_{c} t+frac{pi t}{2 T_{s}} a_{k}+varphi_{k}+psi ight) SMSK​(t)(−sin(ωc​t+ψ))=cos(ωc​t+2Ts​πt​ak​+φk​)(−sin(ωc​t+ψ))=21​sin(2Ts​πt​ak​+φk​−ψ)−21​sin(2ωc​t+2Ts​πt​ak​+φk​+ψ)

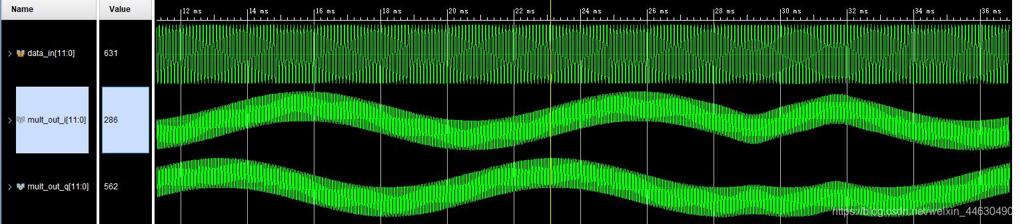
请添加图片描述
抽取滤波，通过CIC抽取滤波器，滤除高频信号，同时对数据进行降采样：
Y 1 = 1 2 cos ⁡ ( π t 2 T s a k + φ k − ψ ) Y 2 = 1 2 sin ⁡ ( π t 2 T s a k + φ k − ψ ) Y_{1}=frac{1}{2} cos left(frac{pi t}{2 T_{s}} a_{k}+varphi_{k}-psi ight) \ Y_{2}=frac{1}{2} sin left(frac{pi t}{2 T_{s}} a_{k}+varphi_{k}-psi ight) Y1​=21​cos(2Ts​πt​ak​+φk​−ψ)Y2​=21​sin(2Ts​πt​ak​+φk​−ψ)

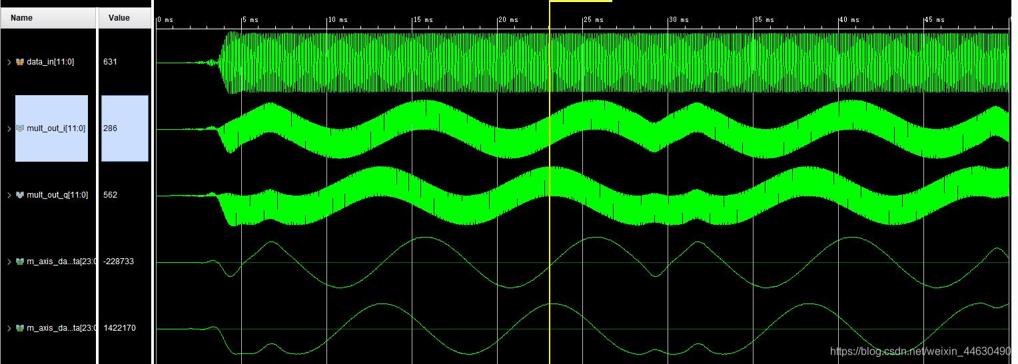
请添加图片描述
Y1和Y2构成的基带信号分别与f1和f2两个正交基函数在一个符号时间内作相关运算：
∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 1 ) d t ∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 2 ) d t int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{1} ight) d t \ int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{2} ight) d t ∫0Ts​​((Y1​+jY2​)⋅f1​)dt∫0Ts​​((Y1​+jY2​)⋅f2​)dt

其中f1和f2为：

f 1 = e j ( π t 2 T s + θ ) f 2 = e − j ( π t 2 T s + θ ) f_{1}=e^{jleft(frac{pi t} {2 T_{s}}+ heta ight)}\ f_{2}=e^{-jleft(frac{pi t}{2 T_{s}}+ heta ight)} f1​=ej(2Ts​πt​+θ)f2​=e−j(2Ts​πt​+θ)

Y 1 + j Y 2 与 f 1 做 相 关 , f 1 中 的 θ 是 一 个 常 量 ， 将 其 归 到 基 带 信 号 的 ψ 中 ， 后 续 不 显 示 了 ， 没 什 么 影 响 : ∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 1 ) d t = ∫ 0 T s ( e j ( π t 2 T s a k + φ k − ψ ) ⋅ e j π t 2 T s ) d t = ∫ 0 T s ( e j ( π t 2 T s ( a k + 1 ) + φ k − ψ ) ) d t Y_{1}+j Y_{2} 与 f_{1} 做相关,f_{1}中的 heta 是一个常量，将其归到基带信号的psi中，后续不显示了，没什么影响: \ int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{1} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{2 T_{s}} a_{k}+varphi_{k}-psi ight)} cdot e^{j frac{pi t}{2 T_{s}}} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{2 T_{s}}left(a_{k}+1 ight)+varphi_{k}-psi ight)} ight) d t Y1​+jY2​与f1​做相关,f1​中的θ是一个常量，将其归到基带信号的ψ中，后续不显示了，没什么影响:∫0Ts​​((Y1​+jY2​)⋅f1​)dt=∫0Ts​​(ej(2Ts​πt​ak​+φk​−ψ)⋅ej2Ts​πt​)dt=∫0Ts​​(ej(2Ts​πt​(ak​+1)+φk​−ψ))dt
Y 1 + j Y 2 与 f 2 做 相 相 关 , f 2 中 的 θ 是 一 个 常 量 ， 将 其 归 到 基 带 信 号 的 ψ 中 ， 后 续 不 显 示 了 ， 没 什 么 影 响 : ∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 2 ) d t = ∫ 0 T s ( e j ( π t 2 T s a k + φ k − ψ ) ⋅ e − j π t 2 T s ) d t = ∫ 0 T s ( e j ( π t 2 T s ( a k − 1 ) + φ k − ψ ) ) d t Y_{1}+j Y_{2} 与 f_{2} 做相相关,f_{2}中的 heta 是一个常量，将其归到基带信号的psi中，后续不显示了，没什么影响: \ int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{2} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{2 T_{s}} a_{k}+varphi_{k}-psi ight)} cdot e^{-j frac{pi t}{2 T_{s}}} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{2 T_{s}}left(a_{k}-1 ight)+varphi_{k}-psi ight)} ight) d t Y1​+jY2​与f2​做相相关,f2​中的θ是一个常量，将其归到基带信号的ψ中，后续不显示了，没什么影响:∫0Ts​​((Y1​+jY2​)⋅f2​)dt=∫0Ts​​(ej(2Ts​πt​ak​+φk​−ψ)⋅e−j2Ts​πt​)dt=∫0Ts​​(ej(2Ts​πt​(ak​−1)+φk​−ψ))dt

当 a k = 1 , Y 1 + j Y 2 与 f 1 相 关 得 ： ∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 1 ) d t = ∫ 0 T s ( e j ( π t 2 T s ( a k + 1 ) + φ k − ψ ) ) d t = ∫ 0 T s ( e j ( π t T s + φ k − ψ ) ) d t 当 a_{k}=1, quad Y_{1}+j Y_{2} 与 f_{1} 相关得：\ int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{1} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{2 T_{s}}left(a_{k}+1 ight)+varphi_{k}-psi ight)} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{T_{s}}+varphi_{k}-psi ight)} ight) d t 当ak​=1,Y1​+jY2​与f1​相关得：∫0Ts​​((Y1​+jY2​)⋅f1​)dt=∫0Ts​​(ej(2Ts​πt​(ak​+1)+φk​−ψ))dt=∫0Ts​​(ej(Ts​πt​+φk​−ψ))dt

当 a k = 1 , Y 1 + j Y 2 与 f 2 相 关 得 : ∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 2 ) d t = ∫ 0 τ s ( e j ( π t 2 τ s ( a k − 1 ) + φ k − ψ ) ) d t = ∫ 0 T s ( e j ( φ k − ψ ) ) d t 当 a_{k}=1, quad Y_{1}+j Y_{2} 与 f_{2} 相关得 :\ int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{2} ight) d t=int_{0}^{ au_{s}}left(e^{jleft(frac{pi t}{2 au_{s}}left(a_{k}-1 ight)+varphi_{k}-psi ight)} ight) d t=int_{0}^{T_{s}}left(e^{jleft(varphi_{k}-psi ight)} ight) d t 当ak​=1,Y1​+jY2​与f2​相关得:∫0Ts​​((Y1​+jY2​)⋅f2​)dt=∫0τs​​(ej(2τs​πt​(ak​−1)+φk​−ψ))dt=∫0Ts​​(ej(φk​−ψ))dt

当 a k = − 1 , Y 1 + j Y 2 与 f 1 相 关 得 : ∫ 0 T s ( ( Y 1 + j Y 2 ) ⋅ f 1 ) d t = ∫ 0 T s ( e j ( π t 2 T S ( a k + 1 ) + φ k − ψ ) ) d t = ∫ 0 τ s ( e j ( φ k − ψ ) ) d t 当 a_{k}=-1, quad Y_{1}+j Y_{2} 与 f_{1} 相关得 :\ int_{0}^{T_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{1} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{2 T_{S}}left(a_{k}+1 ight)+varphi_{k}-psi ight)} ight) d t=int_{0}^{ au_{s}}left(e^{jleft(varphi_{k}-psi ight)} ight) d t 当ak​=−1,Y1​+jY2​与f1​相关得:∫0Ts​​((Y1​+jY2​)⋅f1​)dt=∫0Ts​​(ej(2TS​πt​(ak​+1)+φk​−ψ))dt=∫0τs​​(ej(φk​−ψ))dt

当 a k = − 1 , Y 1 + j Y 2 与 f 2 相 关 得 ： ∫ 0 τ s ( ( Y 1 + j Y 2 ) ⋅ f 2 ) d t = ∫ 0 τ s ( e j ( π t 2 T s ( a k − 1 ) + φ k − ψ ) ) d t = ∫ 0 T s ( e j ( π t T s + φ k − ψ ) ) d t 当 a_{k}=-1, quad Y_{1}+j Y_{2} 与 f_{2} 相关得：\ int_{0}^{ au_{s}}left(left(Y_{1}+j Y_{2} ight) cdot f_{2} ight) d t=int_{0}^{ au_{s}}left(e^{jleft(frac{pi t}{2 T_{s}}left(a_{k}-1 ight)+varphi_{k}-psi ight)} ight) d t=int_{0}^{T_{s}}left(e^{jleft(frac{pi t}{T_{s}}+varphi_{k}-psi ight)} ight) d t 当ak​=−1,Y1​+jY2​与f2​相关得：∫0τs​​((Y1​+jY2​)⋅f2​)dt=∫0τs​​(ej(2Ts​πt​(ak​−1)+φk​−ψ))dt=∫0Ts​​(ej(Ts​πt​+φk​−ψ))dt

————————————————————————————————————————————————————————
即最终都为求两个积分:

∫ 0 T s e j ( φ k − ψ ) d t = T s ⋅ e j ( φ k − ψ ) ∫ 0 T s e j ( π t T s + φ k − ψ ) d t = e j ( φ k − ψ ) ∫ 0 τ s e j π t T s d t = e j ( φ k − ψ ) ⋅ T s j π ⋅ ∫ 0 τ s e j π t T s d j π T s t = e j ( φ k − ψ ) ⋅ T s j π ⋅ e j π t T s ∣ 0 T s = j 2 π ⋅ T s ⋅ e j ( φ k − ψ ) int_{0}^{T_{s}} e^{jleft(varphi_{k}-psi ight)} d t=T_{s} cdot e^{jleft(varphi_{k}-psi ight)} \ int_{0}^{T_{s}} e^{jleft(frac{pi t}{T_{s}}+varphi_{k}-psi ight)} d t=e^{jleft(varphi_{k}-psi ight)} int_{0}^{ au_{s}} e^{j frac{pi t}{T_{s}}} d t=e^{jleft(varphi_{k}-psi ight)} cdot frac{T_{s}}{j pi} cdot int_{0}^{ au_{s}} e^{j frac{pi t}{T_{s}}} d frac{j pi}{T_{s}} t \ =left.e^{jleft(varphi_{k}-psi ight)} cdot frac{T_{s}}{j pi} cdot e^{j frac{pi t}{T_{s}}} ight|_{0} ^{T_{s}}=frac{j 2}{pi} cdot T_{s} cdot e^{jleft(varphi_{k}-psi ight)} ∫0Ts​​ej(φk​−ψ)dt=Ts​⋅ej(φk​−ψ)∫0Ts​​ej(Ts​πt​+φk​−ψ)dt=ej(φk​−ψ)∫0τs​​ejTs​πt​dt=ej(φk​−ψ)⋅jπTs​​⋅∫0τs​​ejTs​πt​dTs​jπ​t=ej(φk​−ψ)⋅jπTs​​⋅ejTs​πt​∣∣∣∣​0Ts​​=πj2​⋅Ts​⋅ej(φk​−ψ)

再进行一定的处理后，根据Y1和Y2可得
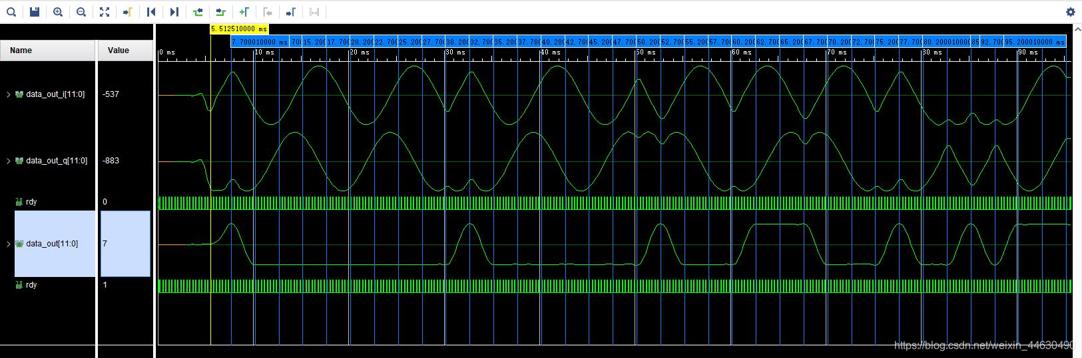
请添加图片描述
由于主要依据接收信号的包络信息进行符号判决，因而该解调算法具有较好的抗相差性能，对信号的适应性强，对载频差要求不严格。

二、突发捕获

在蓝线处抽样判决即可得到ak，但先需要通过m序列准确地检测到信号的起始时刻，才能进行后续处理。利用m序列良好的自相关特性，与本地码做相关运算
请添加图片描述

峰值检测，结果与门限相比较,即可作出判决（门限由阈值和前128个数据的平均值共同得到）
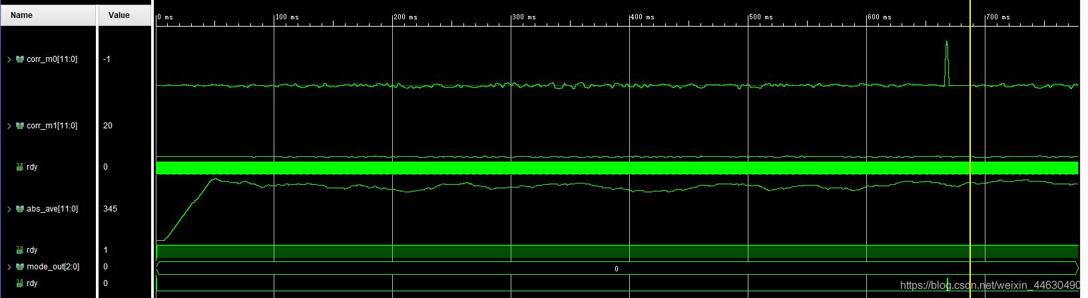
请添加图片描述

三、抽样判决

检测到m序列峰值后，在每一码元的结束时刻进行抽样判决，每组好 1 byte数据，标志位 rdy 有效（拉高），然后将8 bit 数据放入RAM中，为后续RS解码做准备。
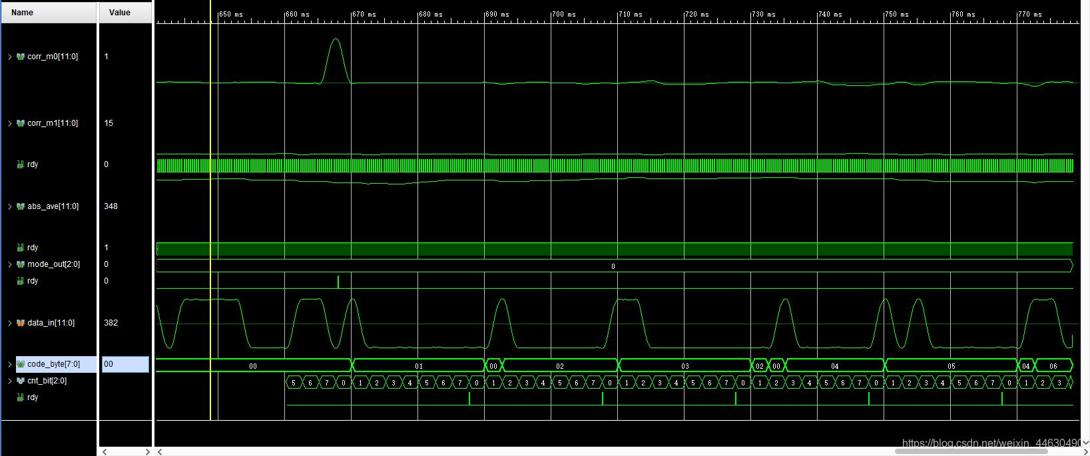
请添加图片描述
突发捕获和抽样判决整体如下所示：
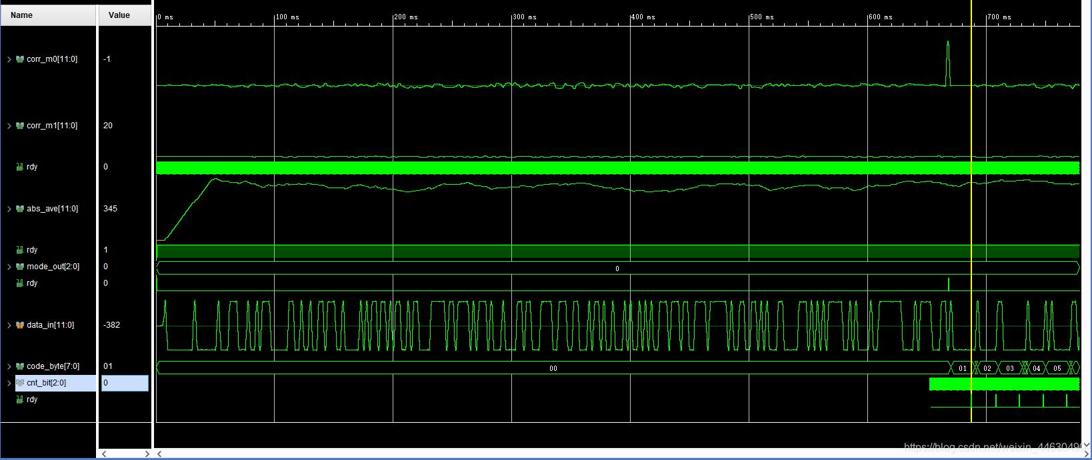
请添加图片描述

四、RS解码

当组完设定的255 byte 后，结束标志位有效，启动RS解码。

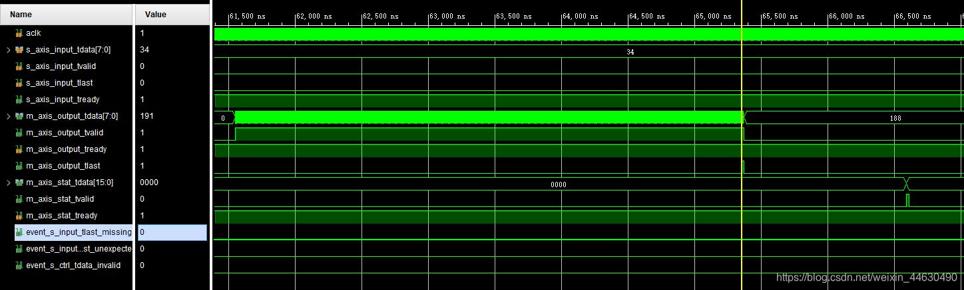
当接收数据未出错时，RS解码数据完全正确，RS解码时序如下，Latency为2606，时钟周期20ns，2606*20ns=52.12us
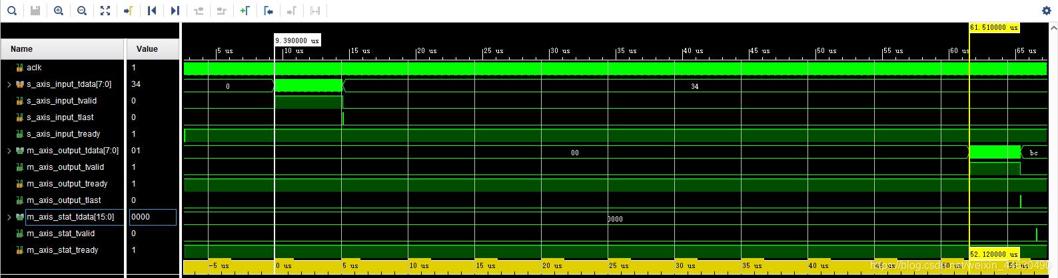
请添加图片描述
接收局部数据如下：
请添加图片描述
RS解码后局部数据如下：
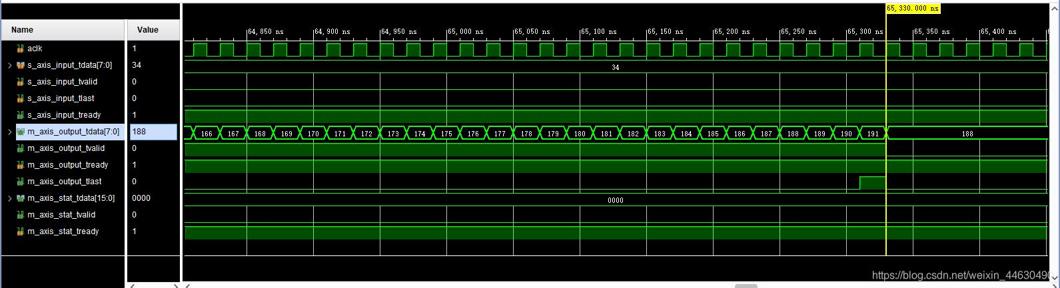
请添加图片描述

当接收数据出现错误时（RS(255，191)，共191个数据，从191数据后为255-191个校验码，第190个数应该是190，现为142），RS解码时将数据纠正回来
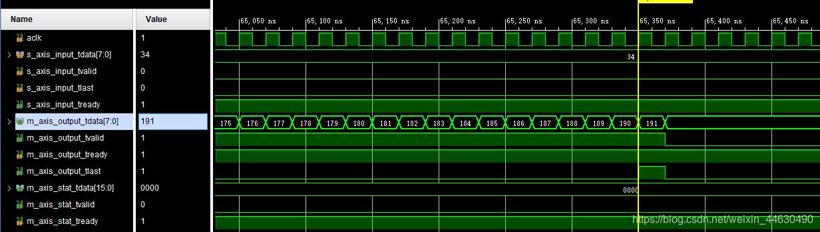
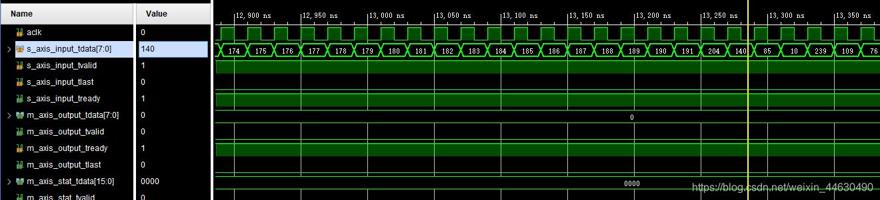
请添加图片描述
请添加图片描述
当接收数据中校验数据出现错误时（RS(255，191)，共191个数据，从191数据后为255-191个校验码，第2个校验数应该是5，现为140），RS解码时也可以将数据纠正

请添加图片描述

请添加图片描述

id="article_content" class="article_content clearfix"> id="content_views" class="htmledit_views">

   如果你想拥有你从未拥有过的东西，那么你必须去做你从未做过的事情

        之前咱们学习了LNMP架构，但是PHP对于技术来说确实是老掉牙了，PHP的市场占有量越来越少了，我认识一个10年的PHP开发工程师，十年工资从15k到今天的6k，现在比较主流的是Java+前端实现界面访问,但是Java需要特定的web服务进行解析展示今天咱们学习tomcat的安装部署，话不多说直接开干~~~~

目录

一、安装java环境，配置tomcat

二、部署Java环境的Tomcat部署zrlog项目

三、搭建LNMT架构（https+nginx负载均衡+mysql数据库+tomcat服务）

四、配置session会话保持

💬欢迎交流：在学习过程中如果你有任何疑问或想法，欢迎在评论区留言，我们可以共同探讨学习的内容。你的支持是我持续创作的动力！

👍点赞、收藏与推荐：如果你觉得这篇文章对你有所帮助，请不要忘记点赞、收藏，并分享给更多的小伙伴！你们的鼓励是我不断进步的源泉！

🚀推广给更多人：如果你认为这篇文章对你有帮助，欢迎分享给更多对Linux感兴趣的朋友，让我们一起进步，共同提升！

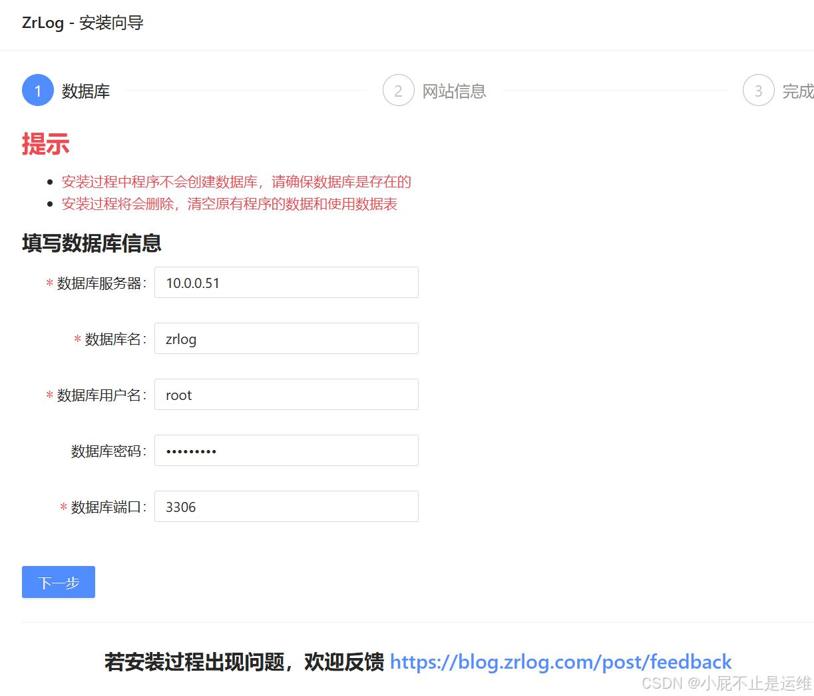
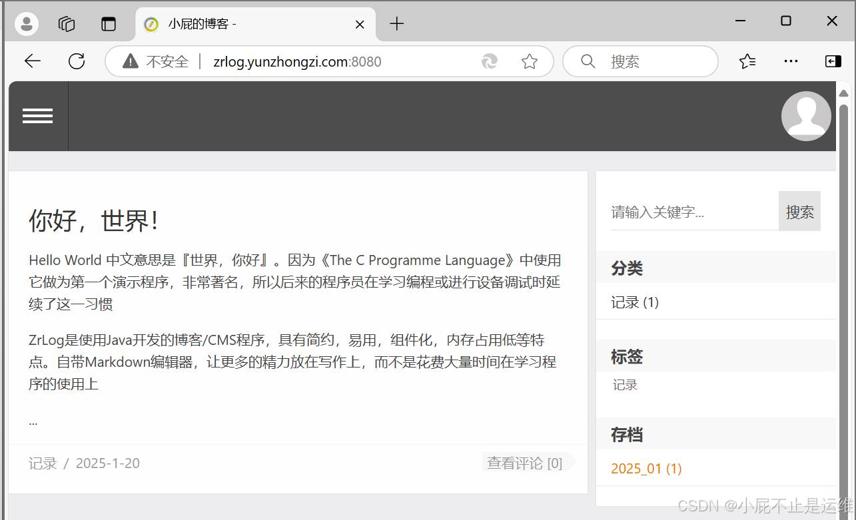
一、安装java环境，配置tomcat

  1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1">
class="hljs-ln-code"> class="hljs-ln-line">安装java环境yum install java -y
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2">
    • class="hljs-ln-code"> class="hljs-ln-line">或者上传rpm包
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">rpm -ivh jdk....rpm
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">查看是否安装成功
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# rpm -qa|grep jdk
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">jdk1.8-1.8.0_181-fcs.x86_64
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">安装tomcat（下载 Tomcat、解压、启动 ）
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">Tomcat官网: https://tomcat.apache.org/
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#wget https://dlcdn.apache.org/tomcat/tomcat-9/v9.0.98/bin/apache-tomcat-9.0.98.tar.gz
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#mkdir /soft
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#tar xf apache-tomcat-9.0.98.tar.gz -C /soft/
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#ln -s /soft/apache-tomcat-9.0.98/ /soft/tomcat
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# /soft/tomcat/bin/startup.sh     # 启动
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# /soft/tomcat/bin/shutdown.sh # 停止
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line"># 8080 对外提供服务的端口 # 8005 关闭Tomcat端口
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# netstat -lntp |grep java
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">tcp6    0    0 127.0.0.1:8005     :::*           LISTEN    6867/java      
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="18"> class="hljs-ln-code"> class="hljs-ln-line">tcp6    0    0 :::8080           :::*           LISTEN    6867/java
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="19"> class="hljs-ln-code"> class="hljs-ln-line">配置systemc方式启动
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="20"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 soft]#vim /usr/lib/systemd/system/tomcat.service
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="21"> class="hljs-ln-code"> class="hljs-ln-line">[Unit]
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="22"> class="hljs-ln-code"> class="hljs-ln-line">Description=Apache Tomcat Server
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="23"> class="hljs-ln-code"> class="hljs-ln-line">After=network.target remote-fs.target nss-lookup.target
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="24"> class="hljs-ln-code"> class="hljs-ln-line">​
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="25"> class="hljs-ln-code"> class="hljs-ln-line">[Service]
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="26"> class="hljs-ln-code"> class="hljs-ln-line">Type=forking
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="27"> class="hljs-ln-code"> class="hljs-ln-line">ExecStart=/soft/tomcat/bin/startup.sh
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="28"> class="hljs-ln-code"> class="hljs-ln-line">ExecStop=/soft/tomcat/bin/shutdown.sh
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="29"> class="hljs-ln-code"> class="hljs-ln-line">ExecRestart=/soft/tomcat/bin/shutdown.sh && sleep2 && /soft/tomcat/bin/star
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="30"> class="hljs-ln-code"> class="hljs-ln-line">tup.sh
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="31"> class="hljs-ln-code"> class="hljs-ln-line">​
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="32"> class="hljs-ln-code"> class="hljs-ln-line">[Install]
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="33"> class="hljs-ln-code"> class="hljs-ln-line">WantedBy=multi-user.target
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="34"> class="hljs-ln-code"> class="hljs-ln-line">重载tomcat，加入开机自启
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="35"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# systemctl daemon-reload
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="36"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#systemctl enable tomcat
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="37"> class="hljs-ln-code"> class="hljs-ln-line">Created symlink from /etc/systemd/system/multi-user.target.wants/tomcat.service to /usr/lib/systemd/system/tomcat.service.
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="38"> class="hljs-ln-code"> class="hljs-ln-line">tomcat配置文件
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="39"> class="hljs-ln-code"> class="hljs-ln-line">tomcat软件目录结构：
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="40"> class="hljs-ln-code"> class="hljs-ln-line">bin          ---主要包含启动和关闭tomcat的脚本（启停java脚本依赖jar包文件）
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="41"> class="hljs-ln-code"> class="hljs-ln-line">conf            ---tomcat配置文件的目录(站点配置：server.xml)
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="42"> class="hljs-ln-code"> class="hljs-ln-line">lib           ---tomcat运行时需要加载的jar包
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="43"> class="hljs-ln-code"> class="hljs-ln-line">logs            ---tomcat日志存放位置
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="44"> class="hljs-ln-code"> class="hljs-ln-line">temp            ---tomcat临时存放文件路径
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="45"> class="hljs-ln-code"> class="hljs-ln-line">webapps       ---tomcat默认站点目录
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="46"> class="hljs-ln-code"> class="hljs-ln-line">work            ---tomcat运行时产生的缓存文件
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="47"> class="hljs-ln-code"> class="hljs-ln-line">​
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="48"> class="hljs-ln-code"> class="hljs-ln-line">关闭防火墙
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="49"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#systemctl stop firewalld.service iptables
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="50"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]#systemctl disable firewalld.service iptables
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="51"> class="hljs-ln-code"> class="hljs-ln-line">​
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="52"> class="hljs-ln-code"> class="hljs-ln-line">​
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="53"> class="hljs-ln-code"> class="hljs-ln-line">测试：添加一个虚拟主机
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="54"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 conf]#vim server.xml
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="55"> class="hljs-ln-code"> class="hljs-ln-line"> "www.yuxiaopi.cn"  appBase="/code/tomcat"
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="56"> class="hljs-ln-code"> class="hljs-ln-line">            unpackWARs="true" autoDeploy="true">
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="57"> class="hljs-ln-code"> class="hljs-ln-line">       "org.apache.catalina.valves.AccessLogValve" directory="logs"
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="58"> class="hljs-ln-code"> class="hljs-ln-line">               prefix="yuxiaopi" suffix=".log"
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="59"> class="hljs-ln-code"> class="hljs-ln-line">               pattern="%h %l %u %t "%r" %s %b" />
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="60"> class="hljs-ln-code"> class="hljs-ln-line">    
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="61"> class="hljs-ln-code"> class="hljs-ln-line">mkdir -p /code/tomcat/ROOT
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="62"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 conf]#echo 学运维找小屁 >/code/tomcat/ROOT/index.html
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="63"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 conf]#vim /code/tomcat/ROOT/index.html
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="64"> class="hljs-ln-code"> class="hljs-ln-line">"1.0" encoding="UTF-8"?>
  • class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="65"> class="hljs-ln-code"> class="hljs-ln-line">学运维找小屁
    •  class="hide-preCode-box"> class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)"> 
    ​

    二、部署Java环境的Tomcat部署zrlog项目

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">定义虚拟主机
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 conf]#vim server.xml 
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">"zrlog.yunzhongzi.com"  appBase="/code/zrlog"    #添加域名和软件存放的位置
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">            unpackWARs="true" autoDeploy="true">
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">​
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">        "org.apache.catalina.valves.AccessLogValve" 
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">directory="logs"
    8.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">               prefix="zrlog" suffix=".log"     #修改日志文件的名称
    9.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">               pattern="%h %l %u %t "%r" %s %b" />
    10.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">      
    11.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">配置环境
    12.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 conf]#mkdir /code/zrlog/ROOT -p
    13.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 conf]#cd /code/zrlog
    14.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">将准备好的ROOT.war文件拖拽至zrlog（环境里可以自动解压war包，如果没解压可以重启tomcat服务）
    15.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line">进入10.0.0.51服务器新建zrlog数据库
    16.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">[root@db01 ~]#mysql -uroot -pqy123.com
    17.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">MariaDB [(none)]> create database zrlog;
    18.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="18"> class="hljs-ln-code"> class="hljs-ln-line">Query OK, 1 row affected (0.01 sec)
    19.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="19"> class="hljs-ln-code"> class="hljs-ln-line">MariaDB [(none)]> show databases;
    20.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="20"> class="hljs-ln-code"> class="hljs-ln-line">+--------------------+
    21.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="21"> class="hljs-ln-code"> class="hljs-ln-line">| Database           |
    22.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="22"> class="hljs-ln-code"> class="hljs-ln-line">+--------------------+
    23.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="23"> class="hljs-ln-code"> class="hljs-ln-line">| information_schema |
    24.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="24"> class="hljs-ln-code"> class="hljs-ln-line">| mysql              |
    25.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="25"> class="hljs-ln-code"> class="hljs-ln-line">| performance_schema |
    26.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="26"> class="hljs-ln-code"> class="hljs-ln-line">| she                |
    27.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="27"> class="hljs-ln-code"> class="hljs-ln-line">| test               |
    28.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="28"> class="hljs-ln-code"> class="hljs-ln-line">| wp                 |
    29.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="29"> class="hljs-ln-code"> class="hljs-ln-line">| zrlog              |
    30.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="30"> class="hljs-ln-code"> class="hljs-ln-line">+--------------------+
    31.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="31"> class="hljs-ln-code"> class="hljs-ln-line">windows端做完hosts解析
    32.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="32"> class="hljs-ln-code"> class="hljs-ln-line">访问zrlog.yunzhongzi.com创建即可
     class="hide-preCode-box"> class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    三、搭建LNMT架构（https+nginx负载均衡+mysql数据库+tomcat服务）

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">配置nfs
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">web01操作如下
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01  ~]# scp -rp /soft  10.0.0.8:/
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01  ~]# scp -rp /code/zrlog  10.0.0.8:/code/zrlog
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# scp /usr/lib/systemd/system/tomcat.service  172.16.1.8:/usr/lib/systemd/system/tomcat.service
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">web02操作如下
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">[root@web02 ~]#ln -s /soft/apache-tomcat-9.0.98/ /soft/tomcat
    8.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">[root@web02 ~]# systemctl daemon-reload
    9.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">[root@web02 ~]# systemctl start tomcat
    10.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">[root@web02 ~]# systemctl enable tomcat
    11.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">Created symlink from /etc/systemd/system/multi-user.target.wants/tomcat.service to /usr/lib/systemd/system/tomcat.service.
    12.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">[root@web02 ~]# yum install nfs-utils -y
    13.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">配置nfs共享目录
    14.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">[root@nfs  ~]# cat /etc/exports
    15.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line">[root@nfs ~]#vim /etc/exports
    16.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">/data 172.16.1.0/24(rw,sync,all_squash,anonuid=666,anongid=666)
    17.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">/code/wp 172.16.1.0/24(rw,sync,all_squash,anonuid=666,anongid=666)
    18.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="18"> class="hljs-ln-code"> class="hljs-ln-line">/code/zrlog 172.16.1.0/24(rw,sync,all_squash,anonuid=666,anongid=666)
    19.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="19"> class="hljs-ln-code"> class="hljs-ln-line">新建挂载的目录
    20.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="20"> class="hljs-ln-code"> class="hljs-ln-line">[root@nfs code]#mkdir zrlog
    21.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="21"> class="hljs-ln-code"> class="hljs-ln-line">修改目录权限
    22.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="22"> class="hljs-ln-code"> class="hljs-ln-line">[root@nfs code]#chown -R www.www zrlog
    23.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="23"> class="hljs-ln-code"> class="hljs-ln-line">[root@nfs code]#ll
    24.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="24"> class="hljs-ln-code"> class="hljs-ln-line">total 0
    25.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="25"> class="hljs-ln-code"> class="hljs-ln-line">drwxr-xr-x 2 www www  6 May  9 22:39 she
    26.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="26"> class="hljs-ln-code"> class="hljs-ln-line">drwxr-xr-x 3 www www 18 Apr 27 20:25 wp
    27.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="27"> class="hljs-ln-code"> class="hljs-ln-line">drwxr-xr-x 2 www www  6 May 10 17:17 zrlog
    28.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="28"> class="hljs-ln-code"> class="hljs-ln-line">重启nfs
    29.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="29"> class="hljs-ln-code"> class="hljs-ln-line">[root@nfs code]#systemctl restart nfs
    30.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="30"> class="hljs-ln-code"> class="hljs-ln-line">挂载（部署playbook的时候写入开机自动挂载）
    31.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="31"> class="hljs-ln-code"> class="hljs-ln-line">[root@web02 image]#mount -t nfs 172.16.1.31:/code/zrlog /code/zrlog/ROOT/attached/
    32.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="32"> class="hljs-ln-code"> class="hljs-ln-line">配置负载均衡
    33.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="33"> class="hljs-ln-code"> class="hljs-ln-line">[root@lb01 conf.d]#vim zrlog.conf 
    34.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="34"> class="hljs-ln-code"> class="hljs-ln-line">upstream zrlog {
    35.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="35"> class="hljs-ln-code"> class="hljs-ln-line">    server 10.0.0.7:8080;
    36.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="36"> class="hljs-ln-code"> class="hljs-ln-line">    server 10.0.0.8:8080;
    37.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="37"> class="hljs-ln-code"> class="hljs-ln-line">}
    38.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="38"> class="hljs-ln-code"> class="hljs-ln-line">server {
    39.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="39"> class="hljs-ln-code"> class="hljs-ln-line">    listen 443 ssl;
    40.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="40"> class="hljs-ln-code"> class="hljs-ln-line">    server_name zrlog.yunzhongzi.com;
    41.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="41"> class="hljs-ln-code"> class="hljs-ln-line">    ssl_certificate ssl_key/server.crt;
    42.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="42"> class="hljs-ln-code"> class="hljs-ln-line">    ssl_certificate_key ssl_key/server.key;
    43.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="43"> class="hljs-ln-code"> class="hljs-ln-line">​
    44.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="44"> class="hljs-ln-code"> class="hljs-ln-line">    location / {
    45.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="45"> class="hljs-ln-code"> class="hljs-ln-line">        proxy_pass http://zrlog;
    46.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="46"> class="hljs-ln-code"> class="hljs-ln-line">        include proxy_params;
    47.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="47"> class="hljs-ln-code"> class="hljs-ln-line">    }
    48.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="48"> class="hljs-ln-code"> class="hljs-ln-line">}
    49.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="49"> class="hljs-ln-code"> class="hljs-ln-line">server {
    50.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="50"> class="hljs-ln-code"> class="hljs-ln-line">    listen 80;
    51.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="51"> class="hljs-ln-code"> class="hljs-ln-line">    server_name zrlog.yunzhongzi.com;
    52.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="52"> class="hljs-ln-code"> class="hljs-ln-line">    return 302 https://$server_name$request_uri;
    53.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="53"> class="hljs-ln-code"> class="hljs-ln-line">}
    54.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="54"> class="hljs-ln-code"> class="hljs-ln-line">密钥文件已经存在服务器直接引用即可（但记得调整web端的服务的属主属组为www）
     class="hide-preCode-box"> class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    四、配置session会话保持

    1.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="1"> class="hljs-ln-code"> class="hljs-ln-line">db01上的redis会话保持功能已经安装完成并开启
    2.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="2"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# wget https://github.com/ran-jit/tomcat-cluster-redis-session-manager/releases/download/4.0/tomcat-cluster-redis-session-manager.zip
    3.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="3"> class="hljs-ln-code"> class="hljs-ln-line">1.解压zip包   
    4.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="4"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# unzip tomcat-cluster-redis-session-manager.zip
    5.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="5"> class="hljs-ln-code"> class="hljs-ln-line">2.拷贝jars到tomcat的/lib目录中
    6.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="6"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# cp tomcat-cluster-redis-session-manager/lib/* /soft/tomcat/lib/
    7.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="7"> class="hljs-ln-code"> class="hljs-ln-line">3.拷贝conf下的redis.properties文件,到tomcat的conf文件
    8.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="8"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# cp tomcat-cluster-redis-session-manager/conf/redis-data-cache.properties /soft/tomcat/conf/
    9.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="9"> class="hljs-ln-code"> class="hljs-ln-line">4.将配置文件中连接redis地址修改为如下地址即可
    10.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="10"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# vim /soft/tomcat/conf/redis-data-cache.properties
    11.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="11"> class="hljs-ln-code"> class="hljs-ln-line">redis.hosts=172.16.1.51:6379
    12.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="12"> class="hljs-ln-code"> class="hljs-ln-line">5.添加如下两行至tomcat/conf/context.xml  (添加在 上一行 )
    13.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="13"> class="hljs-ln-code"> class="hljs-ln-line">[root@web01 ~]# vim /soft/tomcat/conf/context.xml
    14.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="14"> class="hljs-ln-code"> class="hljs-ln-line">"tomcat.request.session.redis.SessionHandlerValve" />
    15.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="15"> class="hljs-ln-code"> class="hljs-ln-line">"tomcat.request.session.redis.SessionManager" />
    16.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="16"> class="hljs-ln-code"> class="hljs-ln-line">注意: 修改完一台直接和另外一台进行无差异同步rsync --delete
    17.  class="hljs-ln-numbers"> class="hljs-ln-line hljs-ln-n" data-line-number="17"> class="hljs-ln-code"> class="hljs-ln-line">修改完成后重启Tomcat
     class="hide-preCode-box"> class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}" onclick="hljs.signin(event)">

    今天的LNMT架构就介绍到这里了，接下来介绍一下nginx的优化和防火墙~~~

    想成为大佬，就要从小白开始，从0开始，一点一点的积累，慢慢成长，明天你就是大佬！！想学习更多麒麟操作系统的知识，关注小屁，让你成为运维老鸟~~~~~ 

    data-report-view="{"mod":"1585297308_001","spm":"1001.2101.3001.6548","dest":"https://blog.csdn.net/weixin_62408089/article/details/145287103","extend1":"pc","ab":"new"}">>
    注：本文转载自blog.csdn.net的lwd_up的文章"https://blog.csdn.net/weixin_44630490/article/details/119060451"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
    复制链接
    复制链接
    相关推荐
    发表评论

    评论记录：

    未查询到任何数据！